Question

If we reduce $3x + 3y + 7 = 0$ to the form $x \cos \alpha + y \sin \alpha = p$, then find the value of $p$.

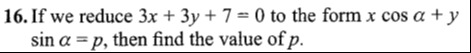
Answer 1

$\frac{7\sqrt{2}}{6}$

Answer 2

The given line is $3x + 3y + 7 = 0$. To convert to the form $x \cos \alpha + y \sin \alpha = p$, we first move the constant term to the right side: $3x + 3y = -7$. Since $p$ must be non-negative, we multiply by $-1$ to make the right side positive: $-3x - 3y = 7$. Now, we divide by $\sqrt{(-3)^2 + (-3)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt{2}$. The equation becomes $\frac{-3x}{3\sqrt{2}} - \frac{3y}{3\sqrt{2}} = \frac{7}{3\sqrt{2}}$. This simplifies to $-\frac{1}{\sqrt{2}}x - \frac{1}{\sqrt{2}}y = \frac{7}{3\sqrt{2}}$. Thus, $p = \frac{7}{3\sqrt{2}}$. Rationalizing the denominator, $p = \frac{7}{3\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{7\sqrt{2}}{6}$.