Question

If p and q are solutions of the equation $5^{(\log_5^2 x)} + x^{\log_5x} = 1250$ then $\log_q p$ has the value equal to-

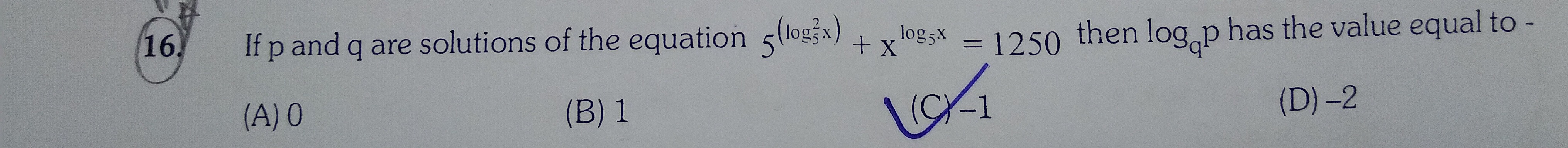
• A. 0
• B. 1
• C. -1
• D. -2

Answer 1

Answer: (C)

The solutions of the equation are $p=25$ and $q=\frac{1}{25}$ (or vice versa). We need to find the value of $\log_q p$. Let $p = 25$ and $q = \frac{1}{25}$. Then $\log_q p = \log_{\frac{1}{25}} 25$. Let $k = \log_{\frac{1}{25}} 25$. By the definition of logarithm, this means $(\frac{1}{25})^k = 25$. We can rewrite $\frac{1}{25}$ as $25^{-1}$. So, $(25^{-1})^k = 25^1$, which implies $25^{-k} = 25^1$. Equating the exponents, we get $-k = 1$, so $k = -1$. If we choose $p = \frac{1}{25}$ and $q = 25$, then $\log_q p = \log_{25} \frac{1}{25} = -1$. Therefore, $\log_q p = -1$.

Answer 2

Let $y = \log_5 x$. Then $x = 5^y$. The given equation is $5^{(\log_5^2 x)} + x^{\log_5x} = 1250$. The term $5^{(\log_5^2 x)}$ can be written as $5^{(\log_5 x)^2} = 5^{y^2}$. The term $x^{\log_5 x}$ can be written as $(5^y)^y = 5^{y^2}$. So the equation becomes $5^{y^2} + 5^{y^2} = 1250$. $2 \cdot 5^{y^2} = 1250$ $5^{y^2} = 625$ $5^{y^2} = 5^4$ $y^2 = 4$ $y = 2$ or $y = -2$.

Case 1: $y = \log_5 x = 2 \implies x = 5^2 = 25$. Case 2: $y = \log_5 x = -2 \implies x = 5^{-2} = \frac{1}{25}$.

The solutions are $p=25$ and $q=\frac{1}{25}$ (or vice versa).

We need to find $\log_q p$. If $p=25$ and $q=\frac{1}{25}$, then $\log_q p = \log_{\frac{1}{25}} 25$. Let $k = \log_{\frac{1}{25}} 25$. $(\frac{1}{25})^k = 25$ $(25^{-1})^k = 25^1$ $25^{-k} = 25^1$ $-k = 1$ $k = -1$.

If $p=\frac{1}{25}$ and $q=25$, then $\log_q p = \log_{25} \frac{1}{25}$. Let $m = \log_{25} \frac{1}{25}$. $25^m = \frac{1}{25}$ $25^m = 25^{-1}$ $m = -1$.

In both cases, $\log_q p = -1$.