Question

Find the range of a if $(a^2, a+1)$ lies between the angle between lines 3x-y+1=0 and x+2y-5=0.

Answer 1

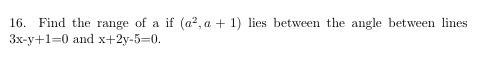
(-\infty, -3) \cup (0, 1/3) \cup (1, \infty)

Answer 2

To find the range of 'a' such that the point $(a^2, a+1)$ lies between the angle formed by the lines $L_1: 3x - y + 1 = 0$ and $L_2: x + 2y - 5 = 0$, we use the condition that for a point $(x_0, y_0)$ to lie in the angle between two lines $A_1x + B_1y + C_1 = 0$ and $A_2x + B_2y + C_2 = 0$, the expressions $(A_1x_0 + B_1y_0 + C_1)$ and $(A_2x_0 + B_2y_0 + C_2)$ must have the same sign. This is equivalent to their product being positive:

$(A_1x_0 + B_1y_0 + C_1)(A_2x_0 + B_2y_0 + C_2) > 0$.

Let the given point be $(x_0, y_0) = (a^2, a+1)$.

Substitute the coordinates of the point into the equations of the lines:

For $L_1$: $3(a^2) - (a+1) + 1 = 3a^2 - a - 1 + 1 = 3a^2 - a$

For $L_2$: $(a^2) + 2(a+1) - 5 = a^2 + 2a + 2 - 5 = a^2 + 2a - 3$

Now, apply the condition:

$(3a^2 - a)(a^2 + 2a - 3) > 0$

Factorize each quadratic expression:

$3a^2 - a = a(3a - 1)$

$a^2 + 2a - 3 = (a+3)(a-1)$

So the inequality becomes:

$a(3a - 1)(a+3)(a-1) > 0$

To solve this inequality, we find the critical points by setting each factor to zero:

$a = 0$

$3a - 1 = 0 \implies a = 1/3$

$a + 3 = 0 \implies a = -3$

$a - 1 = 0 \implies a = 1$

Arrange the critical points in ascending order on a number line: $-3, 0, 1/3, 1$. These points divide the number line into five intervals. We test a value from each interval to determine the sign of the expression $f(a) = a(3a - 1)(a+3)(a-1)$.

1. Interval $(-\infty, -3)$: Let $a = -4$. $f(-4) = (-4)(3(-4)-1)(-4+3)(-4-1) = (-4)(-13)(-1)(-5) = (+) \implies f(a) > 0$

2. Interval $(-3, 0)$: Let $a = -1$. $f(-1) = (-1)(3(-1)-1)(-1+3)(-1-1) = (-1)(-4)(2)(-2) = (-) \implies f(a) < 0$

3. Interval $(0, 1/3)$: Let $a = 0.1$. $f(0.1) = (0.1)(3(0.1)-1)(0.1+3)(0.1-1) = (0.1)(-0.7)(3.1)(-0.9) = (+) \implies f(a) > 0$

4. Interval $(1/3, 1)$: Let $a = 0.5$. $f(0.5) = (0.5)(3(0.5)-1)(0.5+3)(0.5-1) = (0.5)(0.5)(3.5)(-0.5) = (-) \implies f(a) < 0$

5. Interval $(1, \infty)$: Let $a = 2$. $f(2) = (2)(3(2)-1)(2+3)(2-1) = (2)(5)(5)(1) = (+) \implies f(a) > 0$

The inequality $a(3a - 1)(a+3)(a-1) > 0$ holds for the intervals where $f(a)$ is positive.

Therefore, the range of 'a' is $(-\infty, -3) \cup (0, 1/3) \cup (1, \infty)$.

Explanation of the solution:

The point $(x_0, y_0)$ lies in the angle between two lines $L_1=A_1x+B_1y+C_1=0$ and $L_2=A_2x+B_2y+C_2=0$ if $L_1(x_0,y_0)$ and $L_2(x_0,y_0)$ have the same sign, i.e., $L_1(x_0,y_0) \cdot L_2(x_0,y_0) > 0$. Substitute the given point $(a^2, a+1)$ into the line equations to get expressions in 'a': $(3a^2-a)$ and $(a^2+2a-3)$. Set their product to be greater than zero: $(3a^2-a)(a^2+2a-3) > 0$. Factorize the expressions: $a(3a-1)(a+3)(a-1) > 0$. Find the critical points by setting each factor to zero: $-3, 0, 1/3, 1$. Use a sign table or test intervals to determine where the product is positive. The solution is the union of intervals where the expression is positive.