Question
Question: Consider three fixed surfaces shown in the figure. Three blocks each of mass m are released from res...
Consider three fixed surfaces shown in the figure. Three blocks each of mass m are released from rest from top of the three surfaces. All blocks reach ground with same speed. Length of path travelled by the blocks is same for second and third surface. If coefficient of friction of three surfaces are μ1, μ2 and μ3 respectively then
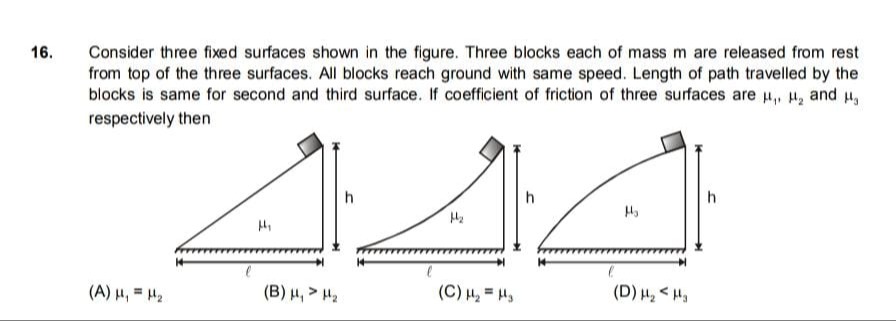
μ1 = μ2
μ1>μ2
μ2=μ3
μ2<μ3
(B) and (D)
Solution
By the work-energy theorem, the work done by friction is the same for all three surfaces since the initial and final kinetic energies, as well as the initial potential energy, are the same.
For surface 1 (straight incline), the work done by friction is Wf1=−μ1N1L1=−μ1(mgcosθ1)L1=−μ1mgl.
For surfaces 2 and 3, the path length is L. Wf2=−μ2∫N2ds=−μ2⟨N2⟩L Wf3=−μ3∫N3ds=−μ3⟨N3⟩L
Since Wf1=Wf2=Wf3, we have μ1mgl=μ2⟨N2⟩L=μ3⟨N3⟩L.
For surface 2 (concave), the normal force is greater than the perpendicular component of gravity (⟨N2⟩>⟨N1⟩). For surface 3 (convex), the normal force is less than the perpendicular component of gravity (⟨N3⟩<⟨N1⟩).
Since μ1⟨N1⟩L1=μ2⟨N2⟩L and L≈L1, and ⟨N2⟩>⟨N1⟩, it implies μ1>μ2.
Since μ1⟨N1⟩L1=μ3⟨N3⟩L and L≈L1, and ⟨N3⟩<⟨N1⟩, it implies μ1<μ3.
Comparing surfaces 2 and 3: μ2⟨N2⟩L=μ3⟨N3⟩L⟹μ2⟨N2⟩=μ3⟨N3⟩. Since ⟨N2⟩>⟨N3⟩, it implies μ2<μ3.
