Question

Charge is uniformly distributed on the curved surface of hemisphere. Potential at P, Q and T is V, V' and V" respectively :-

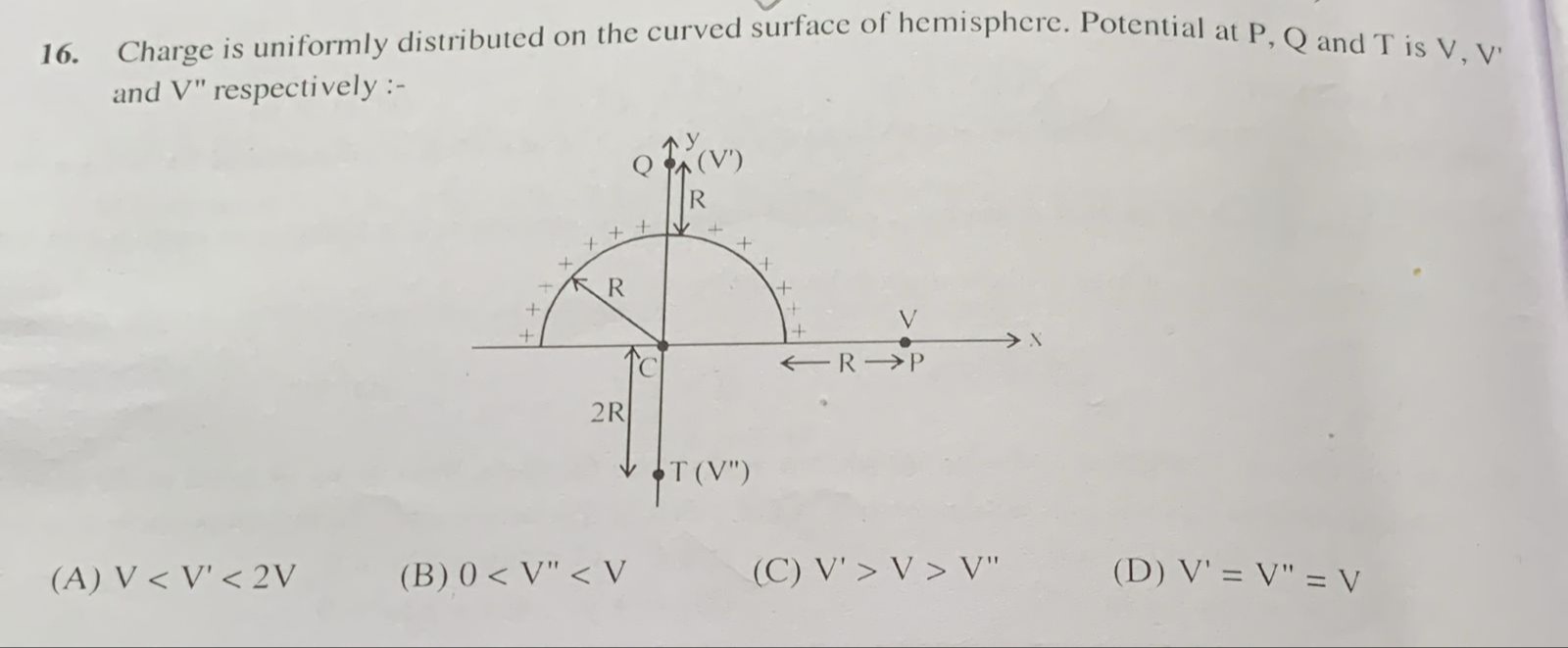
• A. V < V' < 2V
• B. 0 < V" < V
• C. V' > V > V"
• D. V' = V" = V

Answer 1

Answer: (B)

B

Answer 2

The electric potential at a point due to a continuous charge distribution is given by $V = \int \frac{k dq}{r}$, where $dq$ is an infinitesimal charge element and $r$ is the distance from $dq$ to the point.

Let the total charge on the curved surface of the hemisphere be $Q$. The surface area of the curved hemisphere is $2\pi R^2$. The uniform surface charge density is $\sigma = \frac{Q}{2\pi R^2}$.

The center of the base is C, located at the origin (0,0,0). The hemisphere's curved surface is at a constant distance R from C. The potential at C is $V_C = \int \frac{k dq}{R} = \frac{k}{R} \int dq = \frac{kQ}{R}$.

Point P is at (R, 0, 0). Point Q is at (0, R, 0). Point T is at (0, -2R, 0).

Due to the symmetry of the hemisphere about the z-axis, the potential at any point on the x-axis at a distance R from C is the same as the potential at any point on the y-axis at a distance R from C. Thus, the potential at P is equal to the potential at Q.

$V = V'$.

Now let's compare $V$ (or $V'$) and $V''$.

$V = V'$ is the potential at points P and Q, which are at a distance R from the center of the base C.

$V''$ is the potential at point T, which is at a distance 2R from C along the negative y-axis.

Consider the potential at the center C, $V_C = \frac{kQ}{R}$.

Points P and Q are on the circle of radius R centered at C in the x-y plane.

Point T is on the y-axis at a distance 2R from C.

Since the charge is positive, the potential is positive everywhere (except possibly at infinity where it is 0).

As we move away from the charge distribution, the potential generally decreases.

Point T is further away from the hemisphere than points P and Q. So, $V'' < V = V'$.