Solveeit Logo
Login

Question

Question: Use product $\begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix}$ $\begin{bmatrix} ...

Use product [1−1202−33−24]\begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix} [−20192−361−2]\begin{bmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{bmatrix} to solve the system of equations

x - y + 2z = 1

2y - 3z = 1

3x - 2y + 4z = 2

Answer

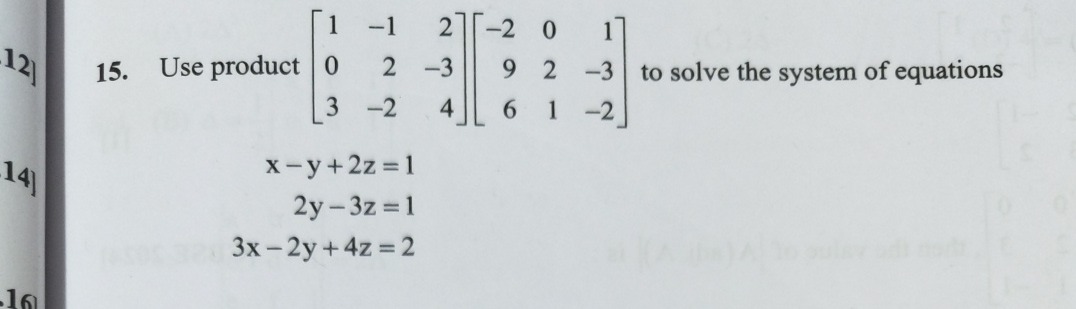
x=0, y=5, z=3

Explanation

Solution

To solve the system of equations using the given product, we follow these steps:

Step 1: Calculate the product of the two given matrices.

Let the first matrix be A and the second matrix be B. A=[1−1202−33−24]A = \begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix} B=[−20192−361−2]B = \begin{bmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{bmatrix}

Calculate the product AB: AB=[(1)(−2)+(−1)(9)+(2)(6)(1)(0)+(−1)(2)+(2)(1)(1)(1)+(−1)(−3)+(2)(−2)(0)(−2)+(2)(9)+(−3)(6)(0)(0)+(2)(2)+(−3)(1)(0)(1)+(2)(−3)+(−3)(−2)(3)(−2)+(−2)(9)+(4)(6)(3)(0)+(−2)(2)+(4)(1)(3)(1)+(−2)(−3)+(4)(−2)]AB = \begin{bmatrix} (1)(-2) + (-1)(9) + (2)(6) & (1)(0) + (-1)(2) + (2)(1) & (1)(1) + (-1)(-3) + (2)(-2) \\ (0)(-2) + (2)(9) + (-3)(6) & (0)(0) + (2)(2) + (-3)(1) & (0)(1) + (2)(-3) + (-3)(-2) \\ (3)(-2) + (-2)(9) + (4)(6) & (3)(0) + (-2)(2) + (4)(1) & (3)(1) + (-2)(-3) + (4)(-2) \end{bmatrix}

AB=[−2−9+120−2+21+3−40+18−180+4−30−6+6−6−18+240−4+43+6−8]AB = \begin{bmatrix} -2 - 9 + 12 & 0 - 2 + 2 & 1 + 3 - 4 \\ 0 + 18 - 18 & 0 + 4 - 3 & 0 - 6 + 6 \\ -6 - 18 + 24 & 0 - 4 + 4 & 3 + 6 - 8 \end{bmatrix}

AB=[100010001]AB = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}

The product AB is the identity matrix, I3I_3. This implies that B is the inverse of A, i.e., B=A−1B = A^{-1}.

Step 2: Write the system of equations in matrix form.

The given system of equations is: x - y + 2z = 1 2y - 3z = 1 3x - 2y + 4z = 2

This can be written in the matrix form AX=CAX = C, where: A=[1−1202−33−24]A = \begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix} (This is the first matrix from the product) X=[xyz]X = \begin{bmatrix} x \\ y \\ z \end{bmatrix} C=[112]C = \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}

Step 3: Solve for X using the inverse matrix.

Since AB=IAB = I, we know that A−1=BA^{-1} = B. To solve AX=CAX = C, we multiply both sides by A−1A^{-1}: A−1AX=A−1CA^{-1}AX = A^{-1}C IX=A−1CIX = A^{-1}C X=A−1CX = A^{-1}C

Substitute the values of A−1A^{-1} (which is B) and C: X=[−20192−361−2][112]X = \begin{bmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}

Perform the matrix multiplication: X=[(−2)(1)+(0)(1)+(1)(2)(9)(1)+(2)(1)+(−3)(2)(6)(1)+(1)(1)+(−2)(2)]X = \begin{bmatrix} (-2)(1) + (0)(1) + (1)(2) \\ (9)(1) + (2)(1) + (-3)(2) \\ (6)(1) + (1)(1) + (-2)(2) \end{bmatrix}

X=[−2+0+29+2−66+1−4]X = \begin{bmatrix} -2 + 0 + 2 \\ 9 + 2 - 6 \\ 6 + 1 - 4 \end{bmatrix}

X=[053]X = \begin{bmatrix} 0 \\ 5 \\ 3 \end{bmatrix}

Step 4: State the solution.

From the matrix X, we get the values of x, y, and z: x = 0 y = 5 z = 3

The final answer is x=0,y=5,z=3\boxed{x=0, y=5, z=3}.

Explanation of the solution:

  1. Matrix Product: Calculate the product of the given matrices. Observe that the product is the identity matrix, implying the second matrix is the inverse of the first.
  2. System in Matrix Form: Represent the given system of linear equations as AX=CAX=C, where A is the coefficient matrix (which is the first matrix from the product), X is the variable matrix, and C is the constant matrix.
  3. Solve using Inverse: Since A−1A^{-1} is known (the second matrix from the product), solve for X using the formula X=A−1CX = A^{-1}C.
  4. Matrix Multiplication: Perform the matrix multiplication to find the values of the variables x, y, and z.