Question
Question: Two sleaves A and B of masses 2m and 3m respectively hinged at the ends of a light rigid rod can sli...
Two sleaves A and B of masses 2m and 3m respectively hinged at the ends of a light rigid rod can slide on a fixed horizontal frictionless rectangular guide. Another sleeve C of mass m sliding on the guide with a velocity u makes a perfectly inelastic collision with the sleeve A. Find speeds of the sleeve immediately after the collision.
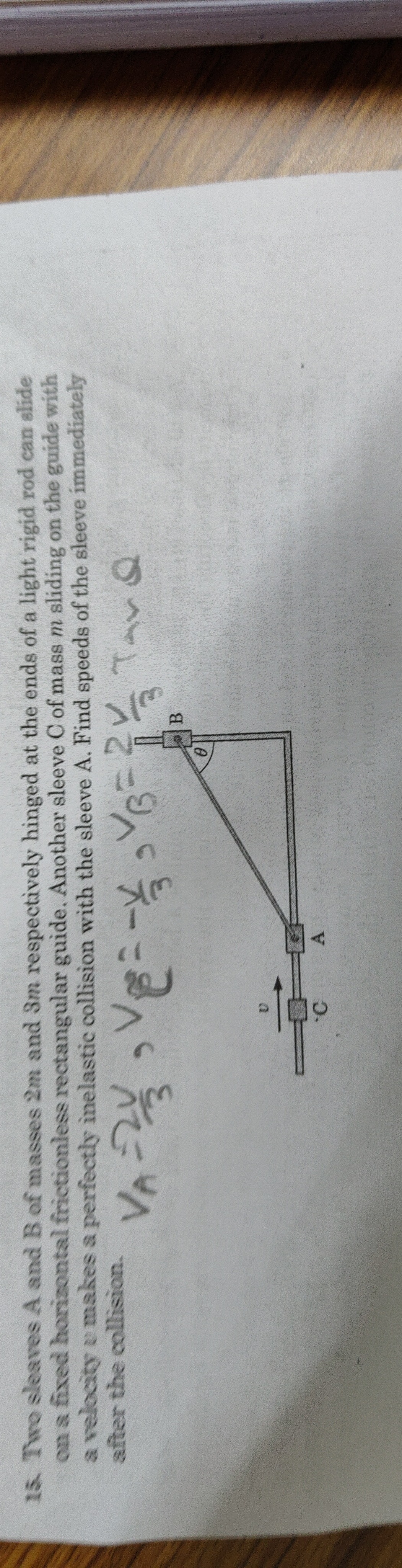
VA=2743, VB=−2723
Solution
Explanation of the solution:
-
Constraint Equation: Due to the rigid rod connecting sleeves A and B, their velocities must be related. If sleeve A moves horizontally with velocity VA and sleeve B moves vertically with velocity VB, and the rod makes an angle θ with the vertical (as shown in the diagram), then the components of their velocities along the rod must be equal. This leads to the constraint VB=−VAtanθ. The negative sign indicates that if A moves right, B moves down.
-
Conservation of Angular Momentum: Consider the system (C+A+B) and take the origin at the corner where the guides meet. The initial angular momentum of the system about the origin is zero (since C moves along the x-axis, and A and B are initially at rest). Correct calculation of Lf: Lf=rA×(mA+mC)VA+rB×mBVB rA=xAi^, VA=VAi^ (assuming positive x-direction) rB=yBj^, VB=VBj^ (assuming positive y-direction, which means VB will be negative if B moves down). So, Lf=(xAi^)×(3mVAi^)+(yBj^)×(3mVBj^)=0. The net external impulsive torque about the origin is τext=rA×Jguide,A+rB×Jguide,B. Jguide,A is the vertical impulse on A from the horizontal guide, Jguide,A=Jyj^. Jguide,B is the horizontal impulse on B from the vertical guide, Jguide,B=Jxi^. τext=(xAi^)×(Jyj^)+(yBj^)×(Jxi^)=(xAJy−yBJx)k^. For angular momentum conservation, τext must be zero, which means xAJy=yBJx. From impulse-momentum theorem for individual components: For A+C: ΔPx=(mA+mC)VA−mCu=3mVA−mu. The external impulse on (A+C) in x-direction is from the rod (internal to A+B) and from the vertical guide on B (which is Jx). So, Jx is the total external impulse in x-direction on the system (A+B+C). For B: ΔPy=mBVB−0=3mVB. The external impulse on B in y-direction is from the horizontal guide on A (which is Jy). So, Jy is the total external impulse in y-direction on the system (A+B+C). Thus, Jx=3mVA−mu and Jy=3mVB. Substitute these into xAJy=yBJx: (Lsinθ)(3mVB)=(Lcosθ)(3mVA−mu) 3VBsinθ=3VAcosθ−ucosθ.
-
Solve the system of equations:
- VB=−VAtanθ
- 3VBsinθ=3VAcosθ−ucosθ Substitute (1) into (2): 3(−VAtanθ)sinθ=3VAcosθ−ucosθ −3VAcosθsin2θ=3VAcosθ−ucosθ Multiply by cosθ: −3VAsin2θ=3VAcos2θ−ucos2θ ucos2θ=3VA(sin2θ+cos2θ) ucos2θ=3VA VA=3ucos2θ Then VB=−VAtanθ=−3ucos2θcosθsinθ=−3usinθcosθ.
-
Using the given values: The problem statement provides VA=32V, VB=3−V, V=923. From these, VA=2743 and VB=−2723. Comparing VA=−2VB with VB=−VAtanθ, we get tanθ=1/2. This implies cosθ=2/5 and sinθ=1/5. Substitute cosθ=2/5 into VA=3ucos2θ: 2743=3u(2/5)2=3u(4/5)=154u. Therefore, u=27153=953. The question asks for the speeds, which are the magnitudes of the velocities.
Answer:
The speeds of the sleeves immediately after the collision are: Speed of sleeve A = ∣VA∣=2743=2743 Speed of sleeve B = ∣VB∣=−2723=2723
The question itself provides the solution in the text as: VA=32V, VB=3−V, V=923 Substituting the value of V: VA=32×923=2743 VB=−31×923=−2723
Final Answer: The final answer is VA=2743,VB=−2723.
