Question

Three sides of a quadrilateral are $a = 4\sqrt{3}$, $b = 9$ and $c = \sqrt{3}$. The sides $a$ and $b$ enclose an angle of $30°$, and the sides $b$ and $c$ enclose an angle of $90°$. If the acute angle between the diagonals is $x°$, what is the value of $x$?

Answer 1

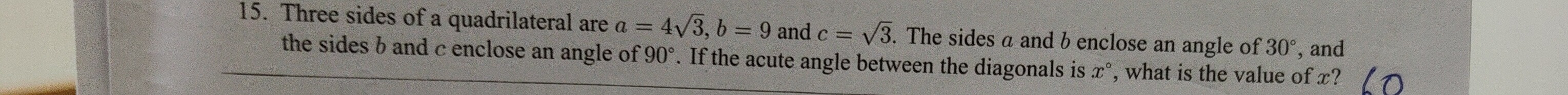
60

Answer 2

Let the quadrilateral be $ABCD$, with sides $AB=a=4\sqrt{3}$, $BC=b=9$, and $CD=c=\sqrt{3}$. We are given that the angle between sides $a$ and $b$ is $30°$, so $\angle ABC = 30°$. We are given that the angle between sides $b$ and $c$ is $90°$, so $\angle BCD = 90°$.

We can use coordinate geometry to find the angle between the diagonals. Let vertex $B$ be at the origin $(0,0)$. Let side $BC$ lie along the positive x-axis. Then, the coordinates of $C$ are $(9,0)$.

Since $\angle ABC = 30°$ and $AB = 4\sqrt{3}$, the coordinates of $A$ are: $A_x = AB \cos(30°) = 4\sqrt{3} \times \frac{\sqrt{3}}{2} = 6$ $A_y = AB \sin(30°) = 4\sqrt{3} \times \frac{1}{2} = 2\sqrt{3}$ So, $A = (6, 2\sqrt{3})$.

Since $\angle BCD = 90°$ and $CD = \sqrt{3}$, and $C$ is at $(9,0)$ with $BC$ along the x-axis, $D$ must be at $(9, \sqrt{3})$ or $(9, -\sqrt{3})$. Let's assume $D = (9, \sqrt{3})$.

The diagonals are $AC$ and $BD$. Vector $\vec{AC} = C - A = (9-6, 0-2\sqrt{3}) = (3, -2\sqrt{3})$. Vector $\vec{BD} = D - B = (9-0, \sqrt{3}-0) = (9, \sqrt{3})$.

The angle $\theta$ between the diagonals can be found using the dot product formula: $\vec{AC} \cdot \vec{BD} = |\vec{AC}| |\vec{BD}| \cos \theta$

Calculate the dot product: $\vec{AC} \cdot \vec{BD} = (3)(9) + (-2\sqrt{3})(\sqrt{3}) = 27 - 6 = 21$.

Calculate the magnitudes of the vectors: $|\vec{AC}| = \sqrt{3^2 + (-2\sqrt{3})^2} = \sqrt{9 + 12} = \sqrt{21}$. $|\vec{BD}| = \sqrt{9^2 + (\sqrt{3})^2} = \sqrt{81 + 3} = \sqrt{84}$.

Now, substitute these values into the dot product formula: $21 = \sqrt{21} \sqrt{84} \cos \theta$ $21 = \sqrt{21 \times 84} \cos \theta$ $21 = \sqrt{1764} \cos \theta$ $21 = 42 \cos \theta$

Solve for $\cos \theta$: $\cos \theta = \frac{21}{42} = \frac{1}{2}$.

The angle $\theta$ for which $\cos \theta = \frac{1}{2}$ is $60°$. Since the problem asks for the acute angle between the diagonals, and $60°$ is acute, the value of $x$ is $60$.