Question
Question: The sum $\frac{C_0}{2}-\frac{C_1}{3}+\frac{C_2}{4}-\frac{C_3}{5}+........$ equals...
The sum 2C0−3C1+4C2−5C3+........ equals
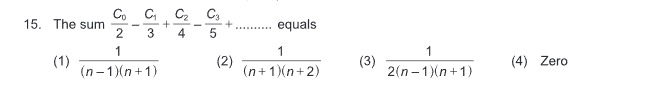
(1) (n−1)(n+1)1
(n+1)(n+2)1
2(n−1)(n+1)1
Zero
(n+1)(n+2)1
Solution
The given sum is S=2C0−3C1+4C2−5C3+......... Assuming Ck=(kn) and the series goes up to k=n, the sum can be written as: S=∑k=0n(−1)kk+2(kn)
We use the integral representation of k+21: k+21=∫01xk+1dx
Substitute this into the sum: S=∑k=0n(−1)k(kn)∫01xk+1dx
Interchange the summation and integration: S=∫01(∑k=0n(−1)k(kn)xk+1)dx S=∫01x(∑k=0n(kn)(−x)k)dx
The sum inside the parenthesis is the binomial expansion of (1−x)n: ∑k=0n(kn)(−x)k=(1−x)n
So, the integral becomes: S=∫01x(1−x)ndx
This integral can be evaluated using substitution. Let u=1−x, so du=−dx. When x=0, u=1. When x=1, u=0. Also, x=1−u. S=∫10(1−u)un(−du) S=∫01(1−u)undu S=∫01(un−un+1)du
Now, integrate term by term: S=[n+1un+1−n+2un+2]01 S=(n+11n+1−n+21n+2)−(0−0) S=n+11−n+21
Combine the fractions: S=(n+1)(n+2)(n+2)−(n+1) S=(n+1)(n+2)1
