Question
Question: The number of real roots of the equation $e^{4x} + e^{3x} - 4e^{2x} + e^x + 1 = 0$ is:...
The number of real roots of the equation e4x+e3x−4e2x+ex+1=0 is:
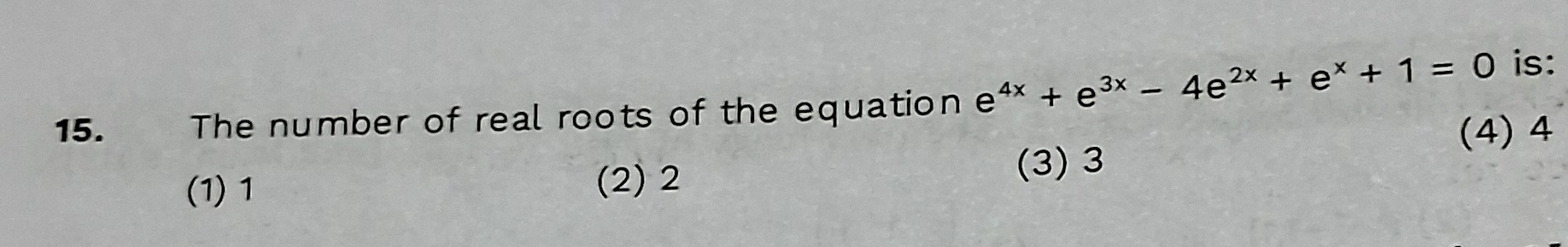
1
2
3
4
1
Solution
Let the given equation be e4x+e3x−4e2x+ex+1=0. Let y=ex. Since x is a real number, ex>0, so y>0. Substituting y into the equation, we get: y4+y3−4y2+y+1=0
This is a quartic equation in y. We are looking for the number of positive real roots of this equation, because each positive real root y corresponds to a unique real root x=lny for the original equation.
The equation is a reciprocal equation since the coefficients (1, 1, -4, 1, 1) are symmetric. Since y=0 is not a root, we can divide the equation by y2: y2+y−4+y1+y21=0 Grouping terms: (y2+y21)+(y+y1)−4=0
Let z=y+y1. Squaring z, we get z2=(y+y1)2=y2+2+y21. So, y2+y21=z2−2.
Substitute this into the equation: (z2−2)+z−4=0 z2+z−6=0
This is a quadratic equation in z. Factoring it, we get: (z+3)(z−2)=0 The possible values for z are z=−3 or z=2.
Now we relate z back to y. We must remember that y>0. For y>0, by the AM-GM inequality, y+y1≥2y⋅y1=2. So, z=y+y1 must satisfy z≥2.
Case 1: z=−3 y+y1=−3. This value z=−3 is less than 2. As expected, this case yields no positive solutions for y. Multiplying by y gives y2+1=−3y, or y2+3y+1=0. The discriminant is Δ=32−4(1)(1)=9−4=5>0. The roots are y=2−3±5. Since 5≈2.236, both roots 2−3+5≈2−0.764 and 2−3−5≈2−5.236 are negative. Since y must be positive, z=−3 yields no valid solutions for y.
Case 2: z=2 y+y1=2. This value z=2 satisfies z≥2. Multiplying by y gives y2+1=2y, or y2−2y+1=0. This equation factors as (y−1)2=0. The only solution is y=1. This is a positive value for y.
So, the only positive root of the polynomial in y is y=1. Now we convert back to x using y=ex: ex=1 x=ln(1) x=0
This is a real root for the original equation. Since y=1 was the only positive root for the polynomial in y, there is only one real root for the original equation.
To confirm, let's check x=0 in the original equation: e4(0)+e3(0)−4e2(0)+e0+1=e0+e0−4e0+e0+1=1+1−4(1)+1+1=1+1−4+1+1=4−4=0. So x=0 is indeed a root.
The number of real roots is 1.
