Question

Solve: $|\log_{\sqrt{3}}x - 2| + |\log_3x - 2| = 2$

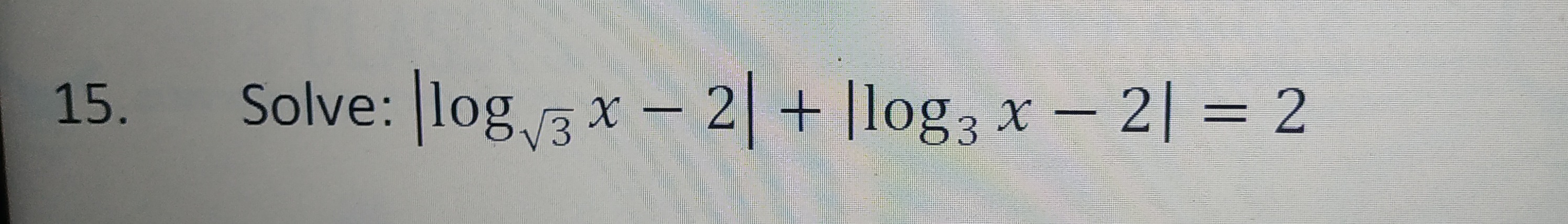
Answer 1

$3^{2/3}, 9$

Answer 2

1. Rewrite $\log_{\sqrt{3}}x$ in terms of $\log_3 x$. $\log_{\sqrt{3}}x = 2 \log_3 x$.

2. Substitute this into the equation: $|2 \log_3 x - 2| + |\log_3 x - 2| = 2$.

3. Let $y = \log_3 x$. The equation becomes $2|y - 1| + |y - 2| = 2$.

4. Solve the absolute value equation $2|y - 1| + |y - 2| = 2$ by considering cases based on $y < 1$, $1 \le y < 2$, and $y \ge 2$.

5. Case 1 ($y < 1$): $2(1-y) + (2-y) = 2 \implies y = 2/3$. Valid.

6. Case 2 ($1 \le y < 2$): $2(y-1) + (2-y) = 2 \implies y = 2$. Not valid in the interval.

7. Case 3 ($y \ge 2$): $2(y-1) + (y-2) = 2 \implies y = 2$. Valid.

8. The solutions for $y$ are $2/3$ and $2$.

9. Convert back to $x$ using $x = 3^y$. $y = 2/3 \implies x = 3^{2/3}$; $y = 2 \implies x = 3^2 = 9$.

10. Verify that the solutions are in the domain $x > 0$. Both $3^{2/3}$ and $9$ are positive.