Question
Question: Solve: $|\log_{\sqrt{3}} x - 2| + |\log_3 x - 2| = 2$...
Solve: ∣log3x−2∣+∣log3x−2∣=2
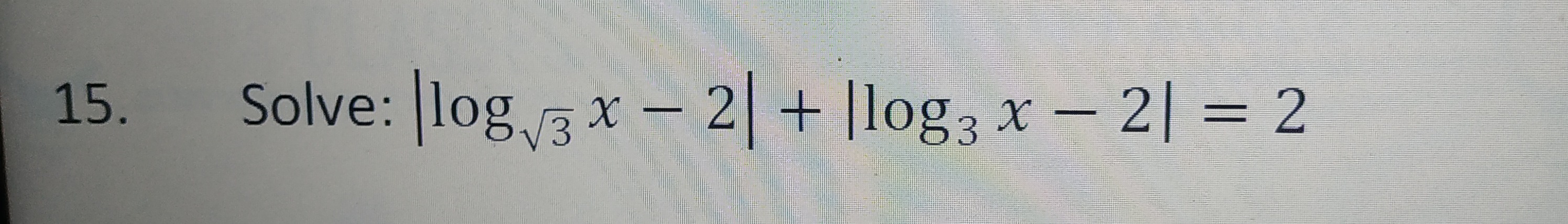
x = 3^{2/3}, 9
Solution
The given equation is ∣log3x−2∣+∣log3x−2∣=2. For the logarithms to be defined, we must have x>0.
First, we express the logarithms in the same base. Let's use base 3. We know that 3=31/2. Using the change of base formula logakb=k1logab, we have: log3x=log31/2x=1/21log3x=2log3x.
Substitute this into the original equation: ∣2log3x−2∣+∣log3x−2∣=2 ∣2(log3x−1)∣+∣log3x−2∣=2 2∣log3x−1∣+∣log3x−2∣=2
Let y=log3x. The equation becomes: 2∣y−1∣+∣y−2∣=2
This is an absolute value equation. We need to consider cases based on the values of y where the expressions inside the absolute values change sign, i.e., the critical points y=1 and y=2.
Case 1: y<1 (i.e., y∈(−∞,1)) In this case, y−1<0 and y−2<0. So, ∣y−1∣=−(y−1)=1−y and ∣y−2∣=−(y−2)=2−y. The equation becomes: 2(1−y)+(2−y)=2 2−2y+2−y=2 4−3y=2 3y=2 y=32 This value y=32 satisfies the condition y<1. So, y=32 is a solution for y.
Case 2: 1≤y<2 (i.e., y∈[1,2)) In this case, y−1≥0 and y−2<0. So, ∣y−1∣=y−1 and ∣y−2∣=−(y−2)=2−y. The equation becomes: 2(y−1)+(2−y)=2 2y−2+2−y=2 y=2 This value y=2 does not satisfy the condition 1≤y<2. So, there are no solutions for y in this interval.
Case 3: y≥2 (i.e., y∈[2,∞)) In this case, y−1≥0 and y−2≥0. So, ∣y−1∣=y−1 and ∣y−2∣=y−2. The equation becomes: 2(y−1)+(y−2)=2 2y−2+y−2=2 3y−4=2 3y=6 y=2 This value y=2 satisfies the condition y≥2. So, y=2 is a solution for y.
Combining the results from all cases, the possible values for y are 32 and 2.
Now we substitute back y=log3x to find the values of x. For y=32: log3x=32 x=32/3 This solution x=32/3=39 is positive, so it is valid.
For y=2: log3x=2 x=32 x=9 This solution x=9 is positive, so it is valid.
The solutions to the equation are x=32/3 and x=9.
