Question

Solve: $\log_{10}^2 x + \log_{10} x^2 = \log_{10}^2 3 -1$

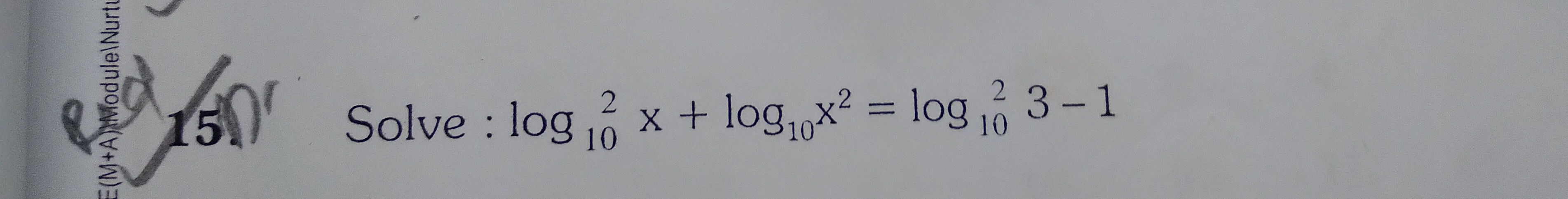
Answer 1

The solutions are $x = \frac{3}{10}$ and $x = \frac{1}{30}$.

Answer 2

Let $y = \log_{10} x$. The equation becomes $y^2 + 2y = (\log_{10} 3)^2 - 1$. Rearranging yields $(y+1)^2 = (\log_{10} 3)^2$. Taking the square root, $y+1 = \pm \log_{10} 3$, so $y = -1 \pm \log_{10} 3$. Substituting back $y = \log_{10} x$:

1. $\log_{10} x = -1 + \log_{10} 3 = \log_{10}(3/10) \implies x = 3/10$.
2. $\log_{10} x = -1 - \log_{10} 3 = -\log_{10}(30) = \log_{10}(1/30) \implies x = 1/30$. Both solutions are positive, satisfying the domain requirement ($x>0$).