Question

Let S be a circle. Tangents are drawn to the circle S from a outside point P points of contacts of tangent are Q and R. A be any point (other than Q and R) on circle S and $l, m, n$ be the length of perpendicular from A to PQ, PR and QR respectively then

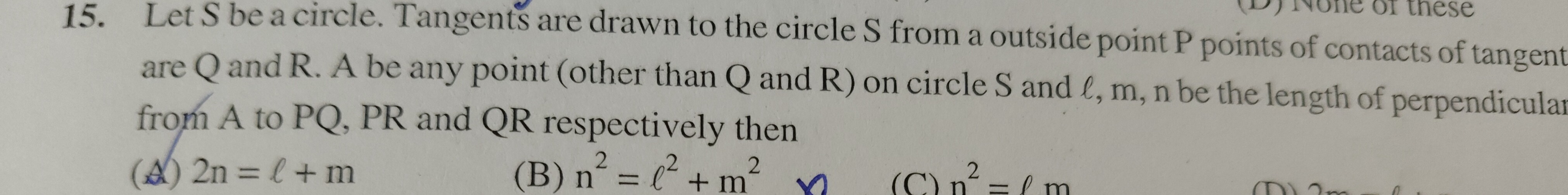
• A. 2n = l + m
• B. n^2 = l^2 + m^2
• C. n^2 = l m
• D. None of these

Answer 1

Answer: (C)

n^2 = l m

Answer 2

Let the circle be $S$ with center $O$ and radius $r$. Let $P$ be an external point. Let $PQ$ and $PR$ be tangents to the circle at points $Q$ and $R$ respectively. $QR$ is the chord of contact. Let $A$ be any point on the circle $S$ (other than $Q$ and $R$). Let $l, m, n$ be the lengths of the perpendiculars from $A$ to $PQ$, $PR$, and $QR$ respectively.

We can place the circle in a coordinate system. Let the circle be $x^2 + y^2 = r^2$. Let $P$ be $(p, 0)$ with $p > r$. The equation of the chord of contact $QR$ is $px + 0y = r^2$, which simplifies to $x = r^2/p$. The tangents $PQ$ and $PR$ have slopes $k = \pm \frac{r}{\sqrt{p^2-r^2}}$. Let these tangents be $T_1$ and $T_2$. The equations of the tangents can be written as $y = k_1(x-p)$ and $y = k_2(x-p)$, where $k_1 = \frac{r}{\sqrt{p^2-r^2}}$ and $k_2 = -\frac{r}{\sqrt{p^2-r^2}}$. In the form $Ax+By+C=0$, these are: $T_1: k_1x - y - k_1p = 0$ $T_2: k_2x - y - k_2p = 0$

Let $A = (x_A, y_A)$ be a point on the circle $x_A^2 + y_A^2 = r^2$. The distance $l$ from $A$ to $PQ$ (say $T_2$) is $l = \frac{|k_2 x_A - y_A - k_2 p|}{\sqrt{k_2^2 + 1}}$. The distance $m$ from $A$ to $PR$ (say $T_1$) is $m = \frac{|k_1 x_A - y_A - k_1 p|}{\sqrt{k_1^2 + 1}}$. The distance $n$ from $A$ to $QR$ (the line $x - r^2/p = 0$) is $n = |x_A - r^2/p|$.

We can simplify the denominators: $k_1^2 + 1 = \frac{r^2}{p^2-r^2} + 1 = \frac{p^2}{p^2-r^2}$, so $\sqrt{k_1^2+1} = \sqrt{k_2^2+1} = \frac{p}{\sqrt{p^2-r^2}}$. Substituting $k_1$ and $k_2$: $l = \frac{|-\frac{r}{\sqrt{p^2-r^2}} x_A - y_A + \frac{r}{\sqrt{p^2-r^2}} p|}{\frac{p}{\sqrt{p^2-r^2}}} = \frac{|-rx_A - \sqrt{p^2-r^2}y_A + rp|}{p}$ $m = \frac{|\frac{r}{\sqrt{p^2-r^2}} x_A - y_A - \frac{r}{\sqrt{p^2-r^2}} p|}{\frac{p}{\sqrt{p^2-r^2}}} = \frac{|rx_A - \sqrt{p^2-r^2}y_A - rp|}{p}$

Let's test the option (C) $n^2 = lm$. $n^2 = \left(x_A - \frac{r^2}{p}\right)^2 = \left(\frac{px_A - r^2}{p}\right)^2 = \frac{(px_A - r^2)^2}{p^2}$. $lm = \frac{|-rx_A - \sqrt{p^2-r^2}y_A + rp|}{p} \cdot \frac{|rx_A - \sqrt{p^2-r^2}y_A - rp|}{p}$ $lm = \frac{|(rp - rx_A) - \sqrt{p^2-r^2}y_A| \cdot |(rp - rx_A) + \sqrt{p^2-r^2}y_A|}{p^2}$ $lm = \frac{|(rp - rx_A)^2 - (p^2-r^2)y_A^2|}{p^2}$ $lm = \frac{|r^2(p-x_A)^2 - (p^2-r^2)y_A^2|}{p^2}$ Using $y_A^2 = r^2 - x_A^2$: $lm = \frac{|r^2(p^2 - 2px_A + x_A^2) - (p^2-r^2)(r^2-x_A^2)|}{p^2}$ $lm = \frac{|r^2p^2 - 2pr^2x_A + r^2x_A^2 - (p^2r^2 - p^2x_A^2 - r^4 + r^2x_A^2)|}{p^2}$ $lm = \frac{|r^2p^2 - 2pr^2x_A + r^2x_A^2 - p^2r^2 + p^2x_A^2 + r^4 - r^2x_A^2|}{p^2}$ $lm = \frac{|-2pr^2x_A + p^2x_A^2 + r^4|}{p^2}$ $lm = \frac{|p^2x_A^2 - 2pr^2x_A + r^4|}{p^2}$ The numerator is $(px_A - r^2)^2$. $lm = \frac{(px_A - r^2)^2}{p^2}$. Thus, $n^2 = lm$ is verified.

This relation $n^2 = lm$ is a known property for a point on a conic section, relating its distances to tangents and the chord of contact.

The final answer is $\boxed{n^2 = l m}$.