Question

Let f be a polynomial function such that $f(3x) = f'(x) \cdot f''(x)$, for all $x \in R$. Then :

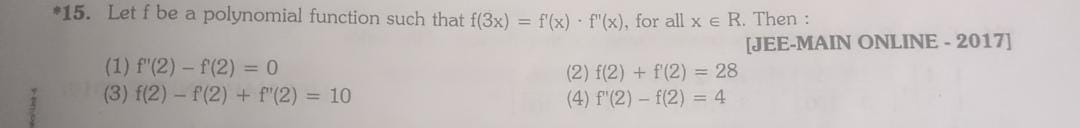
• A. $f'(2) - f(2) = 0$
• B. $f(2) + f'(2) = 28$
• C. $f(2) - f'(2) + f''(2) = 10$
• D. $f''(2) - f(2) = 4$

Answer 1

None of the given options is correct.

Answer 2

We start by assuming that

$$f(x)=ax^3+bx^2+cx+d$$

with $a\ne0$. Then

$$f'(x)=3ax^2+2bx+c \quad \text{and} \quad f''(x)=6ax+2b.$$

Given the functional equation

$$f(3x)=f'(x)f''(x)$$

we compute

$$f(3x)=a(3x)^3+b(3x)^2+c(3x)+d=27ax^3+9bx^2+3cx+d.$$

Also,

$$f'(x)f''(x)=(3ax^2+2bx+c)(6ax+2b).$$

Expanding the product:

$$\begin{aligned} f'(x)f''(x) &= 3ax^2\cdot6ax+3ax^2\cdot2b+2bx\cdot6ax+2bx\cdot2b+c\cdot6ax+c\cdot2b\\[1mm] &= 18a^2x^3 +6abx^2+12abx^2+4b^2x+6acx+2bc\\[1mm] &= 18a^2x^3+18abx^2+(4b^2+6ac)x+2bc. \end{aligned}$$

For the equation to hold for all $x$, the coefficients must match:

1. x^3: $27a=18a^2$ ⟹ $18a^2-27a=0$ ⟹ $9a(2a-3)=0$ $\Rightarrow a=\frac{3}{2}$ (since $a\ne0$).
2. x^2: $9b=18ab$ ⟹ $9b=18\cdot\frac{3}{2}\,b=27b$ ⟹ $9b-27b=0$ ⟹ $b=0$.
3. x^1: $3c=4b^2+6ac$ ⟹ with $b=0$, $3c=6ac=6\cdot\frac{3}{2}\,c=9c$ ⟹ $3c-9c=0$ ⟹ $c=0$.
4. Constant: $d=2bc=0$.

Thus, the unique solution is

$$f(x)=\frac{3}{2}x^3.$$

Now, we compute the required values at $x=2$:

$$f(2)=\frac{3}{2}\cdot8=12,\quad f'(x)=\frac{9}{2}x^2\Rightarrow f'(2)=\frac{9}{2}\cdot4=18,\quad f''(x)=9x\Rightarrow f''(2)=18.$$

Checking the given options:

1. $f'(2)-f(2)=18-12=6$ (not 0).
2. $f(2)+f'(2)=12+18=30$ (not 28).
3. $f(2)-f'(2)+f''(2)=12-18+18=12$ (not 10).
4. $f''(2)-f(2)=18-12=6$ (not 4).

Thus, none of the options is correct.

Assume $f$ cubic. Equate coefficients from $f(3x)=f'(x)f''(x)$ to find $a=\frac{3}{2}, b=c=d=0$. Then compute $f(2)=12,\; f'(2)=18,\; f''(2)=18$, and verify that none of the given expressions match.