Question
Question: Let $\bar{a} \times \bar{b} + \bar{b} = \bar{c} \times \bar{a} + \bar{b} \times \bar{c}$ where $|\ba...
Let aˉ×bˉ+bˉ=cˉ×aˉ+bˉ×cˉ where ∣aˉ∣=∣bˉ∣ then identify the correct statement(s)
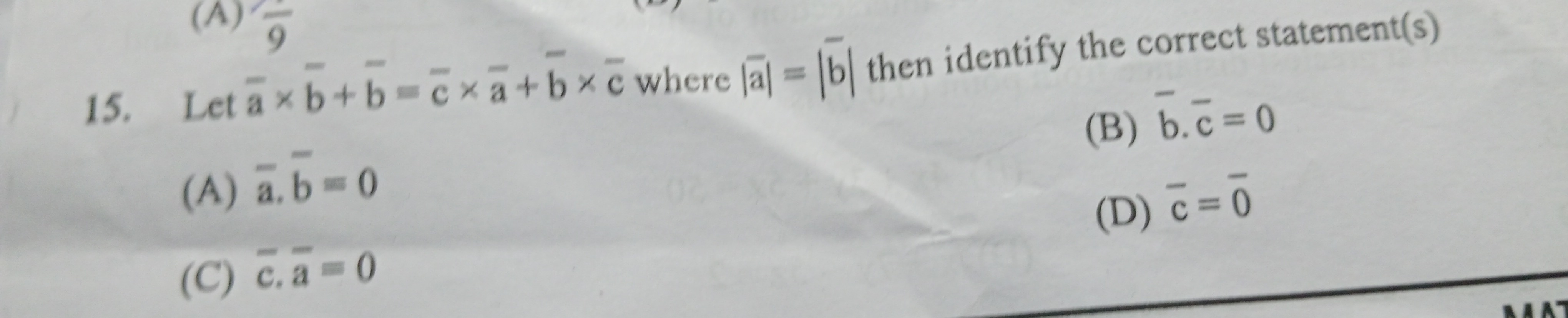
aˉ.bˉ=0
bˉ.cˉ=0
cˉ.aˉ=0
cˉ=0ˉ
A, B, C
Solution
The given equation is aˉ×bˉ+bˉ=cˉ×aˉ+bˉ×cˉ, with the condition ∣aˉ∣=∣bˉ∣.
Rearranging the equation: aˉ×bˉ−cˉ×aˉ−bˉ×cˉ+bˉ=0ˉ
Using the property xˉ×yˉ=−yˉ×xˉ, we have cˉ×aˉ=−aˉ×cˉ and bˉ×cˉ=−cˉ×bˉ. Substituting these into the equation: aˉ×bˉ+aˉ×cˉ+cˉ×bˉ+bˉ=0ˉ aˉ×(bˉ+cˉ)+cˉ×bˉ+bˉ=0ˉ
Taking the dot product of the original equation with bˉ: bˉ⋅(aˉ×bˉ+bˉ)=bˉ⋅(cˉ×aˉ+bˉ×cˉ) bˉ⋅(aˉ×bˉ)+bˉ⋅bˉ=bˉ⋅(cˉ×aˉ)+bˉ⋅(bˉ×cˉ)
Using the property of scalar triple product xˉ⋅(yˉ×xˉ)=0 and xˉ⋅(xˉ×yˉ)=0: 0+∣bˉ∣2=bˉ⋅(cˉ×aˉ)+0 ∣bˉ∣2=bˉ⋅(cˉ×aˉ)
Using the cyclic property of scalar triple product bˉ⋅(cˉ×aˉ)=aˉ⋅(bˉ×cˉ). So, ∣bˉ∣2=aˉ⋅(bˉ×cˉ).
Taking the dot product of the original equation with aˉ: aˉ⋅(aˉ×bˉ+bˉ)=aˉ⋅(cˉ×aˉ+bˉ×cˉ) aˉ⋅(aˉ×bˉ)+aˉ⋅bˉ=aˉ⋅(cˉ×aˉ)+aˉ⋅(bˉ×cˉ) 0+aˉ⋅bˉ=0+aˉ⋅(bˉ×cˉ) aˉ⋅bˉ=aˉ⋅(bˉ×cˉ)
Comparing the results from dot products with aˉ and bˉ: aˉ⋅bˉ=aˉ⋅(bˉ×cˉ) and ∣bˉ∣2=aˉ⋅(bˉ×cˉ). Therefore, aˉ⋅bˉ=∣bˉ∣2. Since ∣aˉ∣=∣bˉ∣, we have aˉ⋅bˉ=∣aˉ∣2.
From aˉ⋅bˉ=∣bˉ∣2, if aˉ⋅bˉ=0, then ∣bˉ∣2=0, which implies bˉ=0ˉ. Since ∣aˉ∣=∣bˉ∣, aˉ=0ˉ.
If aˉ=0ˉ and bˉ=0ˉ, the original equation becomes 0ˉ+0ˉ=0ˉ+0ˉ, which is true. In this case, aˉ⋅bˉ=0⋅0=0.
Also, taking the dot product of the original equation with cˉ: cˉ⋅(aˉ×bˉ+bˉ)=cˉ⋅(cˉ×aˉ+bˉ×cˉ) cˉ⋅(aˉ×bˉ)+cˉ⋅bˉ=cˉ⋅(cˉ×aˉ)+cˉ⋅(bˉ×cˉ) cˉ⋅(aˉ×bˉ)+cˉ⋅bˉ=0+0 cˉ⋅(aˉ×bˉ)+cˉ⋅bˉ=0.
If aˉ=bˉ=0ˉ, then the original equation is satisfied for any cˉ.
In this case: (A) aˉ⋅bˉ=0⋅0=0. True. (B) bˉ⋅cˉ=0⋅cˉ=0. True. (C) cˉ⋅aˉ=cˉ⋅0=0. True. (D) cˉ=0ˉ. Not necessarily true.
Therefore, statements A, B, and C are correct.
