Question
Question: If n(p) = 1x1! + 2x2! + 3x3! + ... nxn! = (n+1) xn! then n is...
If n(p) = 1x1! + 2x2! + 3x3! + ... nxn! = (n+1) xn! then n is
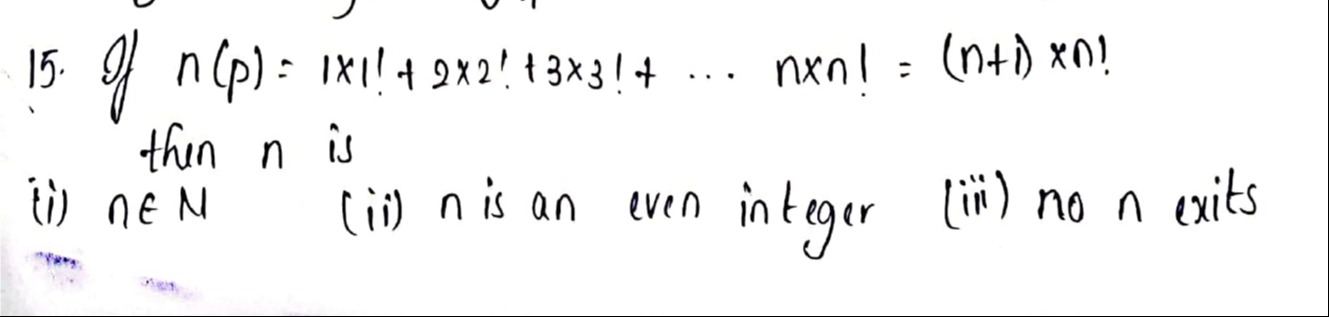
n ∈ N
n is an even integer
no n exits
(iii) no n exists
Solution
The problem asks for which values of 'n' the given equality holds:
1×1!+2×2!+3×3!+⋯+n×n!=(n+1)×n!
Let's evaluate the sum on the left-hand side (LHS). The general term of the sum is k×k!. We can rewrite k×k! as follows:
k×k!=(k+1−1)×k!=(k+1)k!−1×k!=(k+1)!−k!
Now, let's substitute this into the sum: LHS =∑k=1nk×k!=∑k=1n((k+1)!−k!)
This is a telescoping sum: LHS =(2!−1!)+(3!−2!)+(4!−3!)+⋯+((n+1)!−n!) Notice that most terms cancel out: LHS =(n+1)!−1! LHS =(n+1)!−1
Now, let's look at the right-hand side (RHS) of the given equality: RHS =(n+1)×n! By the definition of factorial, (n+1)!=(n+1)×n!. So, RHS =(n+1)!
Now, we equate the LHS and RHS as per the given condition: (n+1)!−1=(n+1)!
To solve for 'n', subtract (n+1)! from both sides of the equation: −1=0
This is a mathematical contradiction. The statement −1=0 is false. This implies that the original equality 1×1!+2×2!+⋯+n×n!=(n+1)×n! is never true for any value of 'n'.
Therefore, no value of 'n' exists for which the given statement holds.
