Question

Find the temperature distribution in the space between two coaxial cylinders of radii $R_1$ and $R_2$ filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to $T_1$ and $T_2$ respectively.

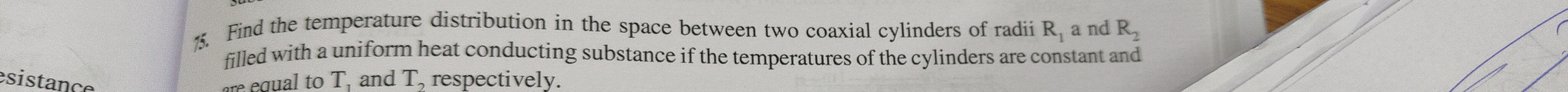
• A. $T(r) = \frac{T_1 \ln(R_2/r) + T_2 \ln(r/R_1)}{\ln(R_2/R_1)}$
• B. $T(r) = T_1 + \frac{T_2 - T_1}{\ln(R_2/R_1)} \ln\left(\frac{r}{R_1}\right)$
• C. $T(r) = \frac{T_1 \ln(r/R_1) + T_2 \ln(R_2/r)}{\ln(R_2/R_1)}$
• D. $T(r) = T_2 + \frac{T_1 - T_2}{\ln(R_1/R_2)} \ln\left(\frac{r}{R_2}\right)$

Answer 1

Answer: (A), (B)

$T(r) = \frac{T_1 \ln(R_2/r) + T_2 \ln(r/R_1)}{\ln(R_2/R_1)}$

Answer 2

The problem involves steady-state heat conduction in a medium with radial symmetry. The governing differential equation in cylindrical coordinates for constant thermal conductivity is: $\frac{1}{r} \frac{d}{dr} \left( r \frac{dT}{dr} \right) = 0$ Integrating this equation twice with respect to $r$ yields the general solution for the temperature distribution: $T(r) = C_1 \ln(r) + C_2$ The constants $C_1$ and $C_2$ are determined using the boundary conditions: $T(R_1) = T_1$ and $T(R_2) = T_2$. Applying the boundary conditions:

1. $T_1 = C_1 \ln(R_1) + C_2$
2. $T_2 = C_1 \ln(R_2) + C_2$

Subtracting equation (1) from equation (2): $T_2 - T_1 = C_1 (\ln(R_2) - \ln(R_1)) = C_1 \ln(R_2/R_1)$ So, $C_1 = \frac{T_2 - T_1}{\ln(R_2/R_1)}$.

Substitute $C_1$ back into equation (1) to find $C_2$: $C_2 = T_1 - C_1 \ln(R_1) = T_1 - \frac{T_2 - T_1}{\ln(R_2/R_1)} \ln(R_1)$.

Substituting $C_1$ and $C_2$ into the general solution: $T(r) = \frac{T_2 - T_1}{\ln(R_2/R_1)} \ln(r) + T_1 - \frac{T_2 - T_1}{\ln(R_2/R_1)} \ln(R_1)$ $T(r) = T_1 + \frac{T_2 - T_1}{\ln(R_2/R_1)} (\ln(r) - \ln(R_1))$ $T(r) = T_1 + \frac{T_2 - T_1}{\ln(R_2/R_1)} \ln\left(\frac{r}{R_1}\right)$ This can be rearranged into a more symmetric form: $T(r) = \frac{T_1 \ln(R_2/R_1) + (T_2 - T_1) \ln(r/R_1)}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 (\ln(R_2) - \ln(R_1)) + T_2 \ln(r/R_1) - T_1 \ln(r/R_1)}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 \ln(R_2) - T_1 \ln(R_1) + T_2 (\ln(r) - \ln(R_1)) - T_1 (\ln(r) - \ln(R_1))}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 \ln(R_2) - T_1 \ln(R_1) + T_2 \ln(r) - T_2 \ln(R_1) - T_1 \ln(r) + T_1 \ln(R_1)}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 \ln(R_2) + T_2 \ln(r) - T_2 \ln(R_1) - T_1 \ln(r)}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 (\ln(R_2) - \ln(r)) + T_2 (\ln(r) - \ln(R_1))}{\ln(R_2/R_1)}$ $T(r) = \frac{T_1 \ln(R_2/r) + T_2 \ln(r/R_1)}{\ln(R_2/R_1)}$