Question

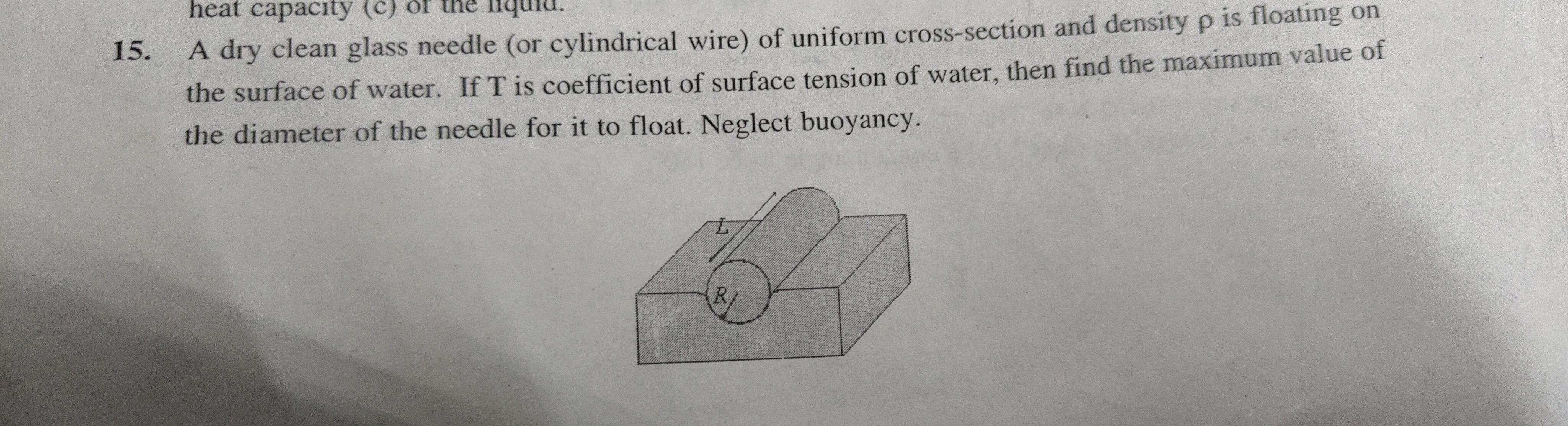
A dry clean glass needle (or cylindrical wire) of uniform cross-section and density $\rho$ is floating on the surface of water. If T is coefficient of surface tension of water, then find the maximum value of the diameter of the needle for it to float. Neglect buoyancy.

Answer 1

$\frac{4T}{L \rho g}$

Answer 2

The weight of the needle is $W = (\pi R^2 L) \rho g$. The upward force due to surface tension is $F_{up} = (2\pi R) T \sin \phi$. For the needle to float, $W \le F_{up}$. The maximum upward force occurs when $\sin \phi = 1$, so $F_{up,max} = 2\pi R T$. Equating weight to maximum upward force for the maximum diameter: $(\pi R^2 L) \rho g = 2\pi R T$. Solving for $R$: $R_{max} = \frac{2T}{L \rho g}$. The maximum diameter is $D_{max} = 2R_{max} = \frac{4T}{L \rho g}$.