Question

A car is moving on a circular path of radius 600 m such that the magnitudes of the tangential acceleration and centripetal acceleration are equal. The time taken by the car to complete first quarter of revolution, if it is moving with an initial speed of 54 km/hr is t(1-e^{-2})s. The value of t is ____.

Answer 1

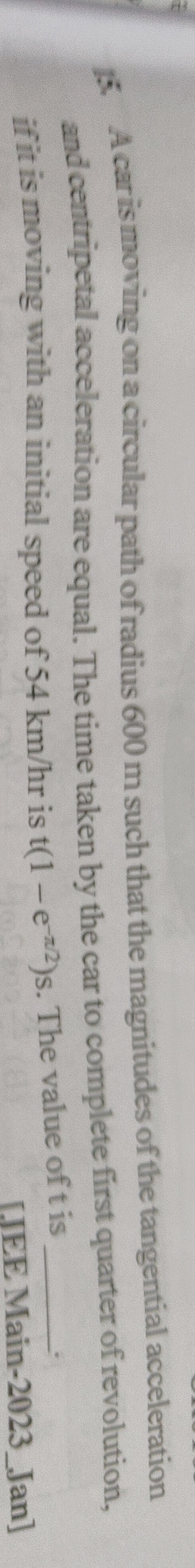
40

Answer 2

1. Convert initial speed: $v_0 = 54 \text{ km/hr} = 15 \text{ m/s}$.

2. Given $a_t = a_c \implies \frac{dv}{dt} = \frac{v^2}{R}$.

3. Using $a_t = v \frac{dv}{ds}$ and $ds = R d\theta$, we get $v \frac{dv}{R d\theta} = \frac{v^2}{R}$.

4. This simplifies to $\frac{dv}{d\theta} = v$, which integrates to $v = v_0 e^\theta$.

5. Substitute $v = R \frac{d\theta}{dt}$ into $v = v_0 e^\theta$ to get $R \frac{d\theta}{dt} = v_0 e^\theta$.

6. Rearrange and integrate for time: $dt = \frac{R}{v_0} e^{-\theta} d\theta$.

7. Integrate from $\theta=0$ to $\theta=\frac{\pi}{2}$ (first quarter revolution):

   $t_{total} = \int_{0}^{\pi/2} \frac{R}{v_0} e^{-\theta} d\theta = \frac{R}{v_0} [ -e^{-\theta} ]_0^{\pi/2} = \frac{R}{v_0} (1 - e^{-\pi/2})$.

8. Substitute $R=600 \text{ m}$ and $v_0=15 \text{ m/s}$:

   $t_{total} = \frac{600}{15} (1 - e^{-\pi/2}) = 40 (1 - e^{-\pi/2}) \text{ s}$.

9. Comparing this with the given form $t(1 - e^{-2}) \text{ s}$, and noting the similar question's form $t(1 - e^{-\pi/2}) \text{ s}$ with answer 40, it is concluded that the exponent $-2$ is a typo and should be $-\frac{\pi}{2}$.

10. Therefore, $t = 40$.