Question

148. A r.v. X assumes values 1, 2, 3, ... n with equal probabilities. what will be n if Var(X) = E(X)?

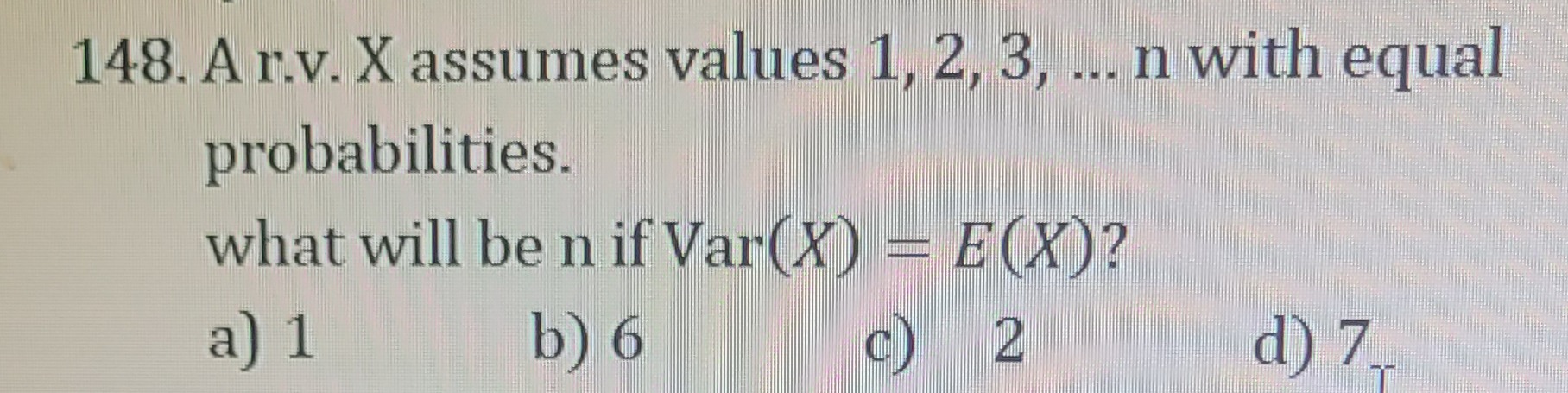
• A. 1
• B. 6
• C. 2
• D. 7

Answer 1

Answer: (D)

7

Answer 2

For a discrete uniform distribution from 1 to n, we have:

$$E(X)=\frac{n+1}{2} \quad \text{and} \quad Var(X)=\frac{n^2-1}{12}$$

Setting $Var(X) = E(X)$:

$$\frac{n^2-1}{12} = \frac{n+1}{2}$$

Multiply both sides by 12:

$$n^2-1=6(n+1)$$

Simplify:

$$n^2 - 6n - 7 = 0$$

Solving the quadratic equation:

$$n = \frac{6 \pm \sqrt{36+28}}{2} = \frac{6 \pm 8}{2}$$

Taking the positive value:

$$n=7$$