Question
Question: $\cos \left[\sin^{-1}\left(\frac{3}{5}\right) + \cos^{-1}\left(\frac{12}{13}\right)\right] =$...
cos[sin−1(53)+cos−1(1312)]=
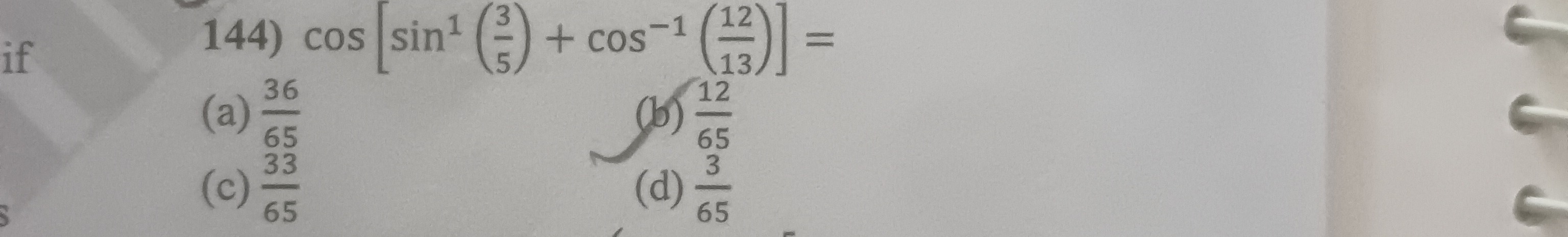
A
6536
B
6512
C
6533
D
653
Answer
6533
Explanation
Solution
Let
α=sin−1(53) and β=cos−1(1312).
Then:
sinα=53 and cosα=1−(53)2=54;
cosβ=1312 and sinβ=1−(1312)2=135.
Using the cosine addition formula:
cos(α+β)=cosαcosβ−sinαsinβ=54⋅1312−53⋅135=6548−6515=6533.
