Question

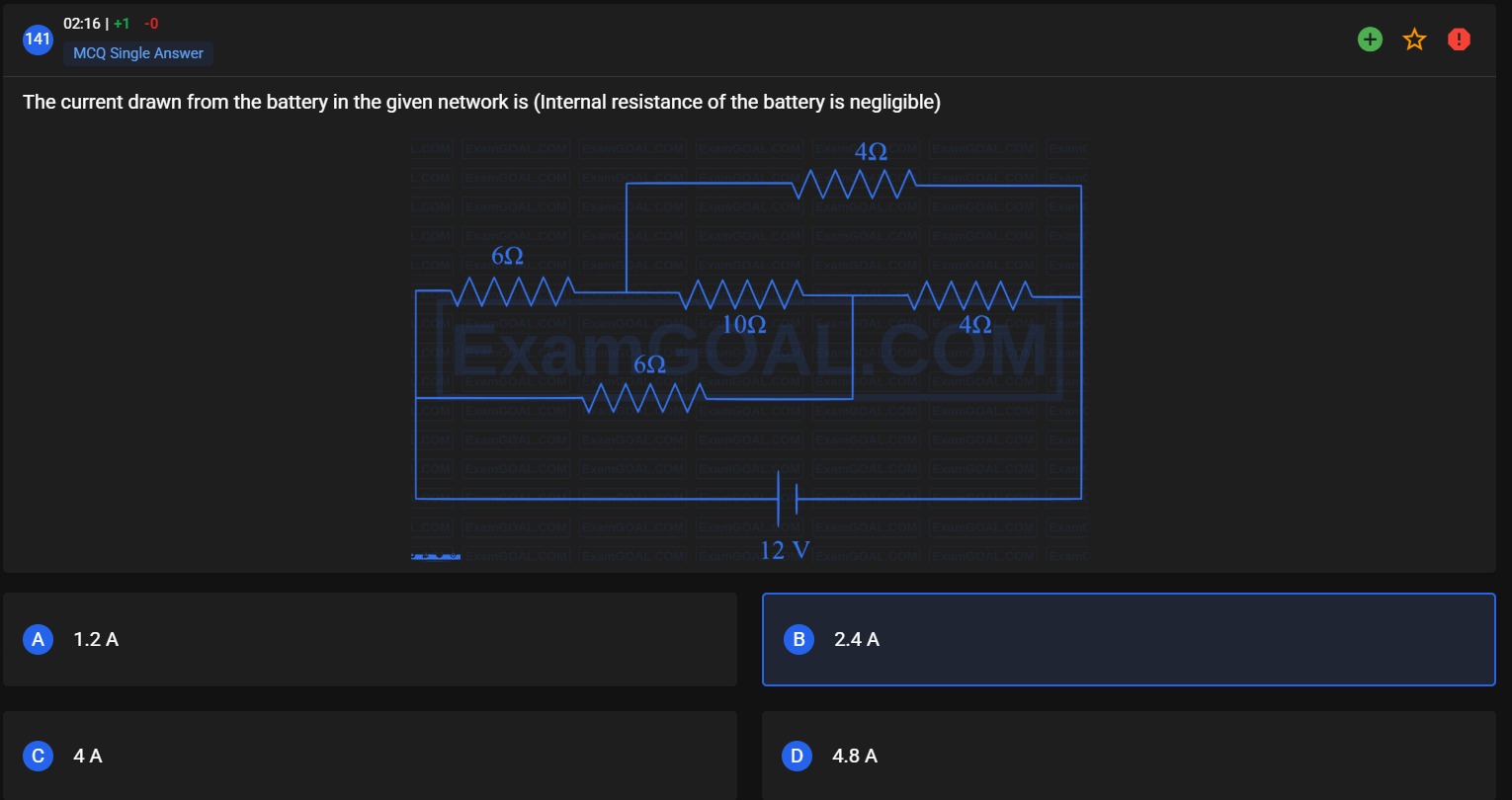
The current drawn from the battery in the given network is (Internal resistance of the battery is negligible)

• A. 1.2 A
• B. 2.4 A
• C. 4 A
• D. 4.8 A

Answer 1

Answer: (B)

2.4 A

Answer 2

1. Top branch: Resistors in series:

   $$R_{top} = 6\Omega + 4\Omega = 10\Omega.$$

2. Bottom branch assumption: The wording suggests the 10Ω and 4Ω resistors are in parallel, then in series with the 6Ω. Calculate the parallel combination:

   $$R_{34} = \frac{10\Omega \times 4\Omega}{10\Omega+4\Omega} = \frac{40}{14} = \frac{20}{7}\Omega \approx 2.857\Omega.$$

   Then,

   $$R_{bottom} = 6\Omega + \frac{20}{7}\Omega = \frac{42+20}{7}\Omega = \frac{62}{7}\Omega \approx 8.857\Omega.$$

3. Equivalent resistance of parallel branches:

   $$\frac{1}{R_{eq}}=\frac{1}{10\Omega}+\frac{1}{(62/7)\Omega} =\frac{1}{10}+\frac{7}{62}.$$

   Calculate:

   $$\frac{1}{R_{eq}} = 0.1 + 0.1129 \approx 0.2129 \quad\Longrightarrow\quad R_{eq} \approx \frac{1}{0.2129} \approx 4.70\Omega.$$

4. Current from the battery:

   $$I=\frac{V}{R_{eq}}=\frac{12\,V}{4.70\Omega}\approx2.55\,A.$$

5. Choosing the best option: Among the options, the closest answer is 2.4 A.