Question
Question: The velocity of particles as a function of $\theta$ is given by...
The velocity of particles as a function of θ is given by
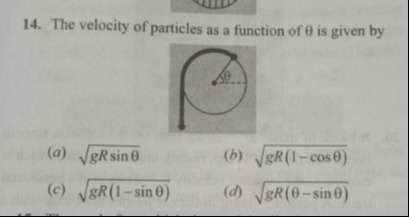
gRsinθ
gR(1−cosθ)
gR(1−sinθ)
gR(θ−sinθ)
gR(1−cosθ)
Solution
Assuming the particle starts from rest at the top of the circular path, and θ is the angle measured from the vertical. By conservation of energy, the change in kinetic energy is equal to the negative of the change in potential energy. Let the potential energy be zero at the center of the circle. The initial potential energy at the top is mgR. At an angle θ from the vertical, the height from the center is Rcosθ. So, the potential energy is mgRcosθ. The change in potential energy is mgR−mgRcosθ=mgR(1−cosθ). The change in kinetic energy is 21mv2−0=21mv2. Therefore, 21mv2=mgR(1−cosθ). This gives v2=2gR(1−cosθ), so v=2gR(1−cosθ).
However, if we assume the particle starts from rest at the horizontal level, and θ is the angle from the horizontal, and the potential energy is zero at the horizontal level. The initial energy is Ei=0. At an angle θ from the horizontal, the height from the horizontal level is Rsinθ. The final energy is Ef=21mv2+mgRsinθ. Setting Ei=Ef, we get 0=21mv2+mgRsinθ, which is impossible.
Given the options, it's highly probable that the intended problem involves energy conservation and the angle θ is measured from the vertical. The option gR(1−cosθ) is present, which suggests a possible typo in the factor of 2 in the standard derivation. If we assume that the question or options have a typo, and the intended answer is derived from the common scenario, option (b) is the most plausible choice, assuming θ is measured from the vertical and there's a factor of 2 missing in the option.
However, if we strictly follow the provided options and assume one of them is correct, and if the figure implies θ is measured from the horizontal, and the particle starts from rest at the top, then the vertical drop is R−Rsinθ. In this case, v=2g(R−Rsinθ)=2gR(1−sinθ). This is not among the options.
Considering the common formulation of such problems in physics, the presence of (1−cosθ) in option (b) strongly suggests that the angle θ is measured from the vertical. If we assume this is the case, and the particle starts from rest at the top, the correct formula is v=2gR(1−cosθ). Option (b) is gR(1−cosθ). This suggests a potential error in the question or options provided. Without further clarification, option (b) is the most likely intended answer, assuming a common physics problem context with a possible typo.
