Question

The sum of the distances of the point P lying inside the triangle formed by lines y = 0; 4x - 3y = 0 and 3x + 4y - 9 = 0 is 3. Then the locus of P is-

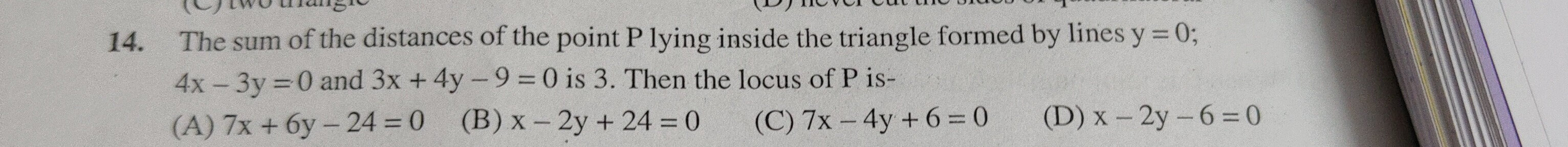
• A. 7x + 6y - 24 = 0
• B. x - 2y + 24 = 0
• C. 7x – 4y + 6 = 0
• D. x - 2y - 6 = 0

Answer 1

Answer: (D)

x - 2y - 6 = 0

Answer 2

To find the locus of point P(x, y) lying inside the triangle formed by the given lines, we first need to identify the lines and the region "inside the triangle".

The three lines are:

1. $L_1: y = 0$
2. $L_2: 4x - 3y = 0$
3. $L_3: 3x + 4y - 9 = 0$

The distance of a point $(x_0, y_0)$ from a line $Ax + By + C = 0$ is given by the formula $d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.

Let $d_1, d_2, d_3$ be the distances of P(x, y) from $L_1, L_2, L_3$ respectively.

1. Distance from $L_1: y = 0$: $d_1 = \frac{|y|}{\sqrt{0^2 + 1^2}} = |y|$
2. Distance from $L_2: 4x - 3y = 0$: $d_2 = \frac{|4x - 3y|}{\sqrt{4^2 + (-3)^2}} = \frac{|4x - 3y|}{\sqrt{16 + 9}} = \frac{|4x - 3y|}{5}$
3. Distance from $L_3: 3x + 4y - 9 = 0$: $d_3 = \frac{|3x + 4y - 9|}{\sqrt{3^2 + 4^2}} = \frac{|3x + 4y - 9|}{\sqrt{9 + 16}} = \frac{|3x + 4y - 9|}{5}$

The problem states that the sum of these distances is 3: $d_1 + d_2 + d_3 = 3$ $|y| + \frac{|4x - 3y|}{5} + \frac{|3x + 4y - 9|}{5} = 3$

Now, we need to determine the signs of the expressions inside the absolute values for a point P lying inside the triangle.

First, let's find the vertices of the triangle:

• Intersection of $L_1 (y=0)$ and $L_2 (4x-3y=0)$: Substitute $y=0$ into $4x-3y=0 \implies 4x=0 \implies x=0$. Vertex A = (0, 0).
• Intersection of $L_1 (y=0)$ and $L_3 (3x+4y-9=0)$: Substitute $y=0$ into $3x+4y-9=0 \implies 3x-9=0 \implies x=3$. Vertex B = (3, 0).
• Intersection of $L_2 (4x-3y=0)$ and $L_3 (3x+4y-9=0)$: From $L_2$, $y = \frac{4}{3}x$. Substitute into $L_3$: $3x + 4\left(\frac{4}{3}x\right) - 9 = 0$ $3x + \frac{16}{3}x - 9 = 0$ $\frac{9x + 16x}{3} = 9$ $\frac{25x}{3} = 9 \implies x = \frac{27}{25}$. Then $y = \frac{4}{3} \times \frac{27}{25} = \frac{4 \times 9}{25} = \frac{36}{25}$. Vertex C = $(\frac{27}{25}, \frac{36}{25})$.

The vertices are A(0,0), B(3,0), C($\frac{27}{25}, \frac{36}{25}$). The triangle lies in the first quadrant.

Consider a point P(x, y) inside this triangle:

1. For $y = 0$: Since P is inside the triangle and the base is on $y=0$, any point inside must have $y > 0$. So, $|y| = y$.
2. For $4x - 3y = 0$: This line passes through the origin (vertex A). To determine the sign for points inside the triangle, pick a test point, e.g., the centroid $(\frac{34}{25}, \frac{12}{25})$. For this point, $4x - 3y = 4(\frac{34}{25}) - 3(\frac{12}{25}) = \frac{136 - 36}{25} = \frac{100}{25} = 4 > 0$. So, for points inside the triangle, $4x - 3y > 0$. Thus, $|4x - 3y| = 4x - 3y$.
3. For $3x + 4y - 9 = 0$: Test the origin (0,0), which is a vertex. $3(0) + 4(0) - 9 = -9 < 0$. Since the triangle lies on the side of $L_3$ that contains the origin, for points inside the triangle, $3x + 4y - 9 < 0$. Thus, $|3x + 4y - 9| = -(3x + 4y - 9) = 9 - 3x - 4y$.

Substitute these expressions back into the sum of distances equation: $y + \frac{4x - 3y}{5} + \frac{9 - 3x - 4y}{5} = 3$

Multiply the entire equation by 5 to clear the denominators: $5y + (4x - 3y) + (9 - 3x - 4y) = 15$

Combine like terms: $(4x - 3x) + (5y - 3y - 4y) + 9 = 15$ $x + (2y - 4y) + 9 = 15$ $x - 2y + 9 = 15$ $x - 2y = 15 - 9$ $x - 2y = 6$ $x - 2y - 6 = 0$

This is the equation of the locus of point P.