Question

The product of perpendiculars drawn from the point (1, 2) to the pair of lines $x^2 + 4xy + y^2 = 0$ is :

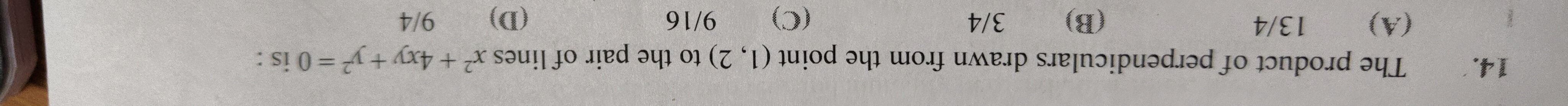
• A. 13/4
• B. 3/4
• C. 9/16
• D. 9/4

Answer 1

Answer: (A)

13/4

Answer 2

The given equation $x^2 + 4xy + y^2 = 0$ represents a pair of lines passing through the origin. This is a homogeneous equation of the form $ax^2 + 2hxy + by^2 = 0$, where $a=1$, $2h=4$ (so $h=2$), and $b=1$.

The product of the perpendicular distances from a point $(x_0, y_0)$ to the pair of lines $ax^2 + 2hxy + by^2 = 0$ is given by the formula: $p_1 p_2 = \frac{|ax_0^2 + 2hx_0y_0 + by_0^2|}{\sqrt{(a-b)^2 + (2h)^2}}$ In this problem, the point is $(x_0, y_0) = (1, 2)$. Substituting the values: $a=1$, $2h=4$, $b=1$, $x_0=1$, $y_0=2$.

The numerator is: $|ax_0^2 + 2hx_0y_0 + by_0^2| = |1(1)^2 + 4(1)(2) + 1(2)^2|$ $= |1 + 8 + 4| = |13| = 13$.

The denominator is: $\sqrt{(a-b)^2 + (2h)^2} = \sqrt{(1-1)^2 + (4)^2}$ $= \sqrt{0^2 + 16} = \sqrt{16} = 4$.

Therefore, the product of the perpendiculars is: $p_1 p_2 = \frac{13}{4}$