Solveeit Logo
Login

Question

Question: The numbers of integral solutions of D = 8, where D = $\begin{vmatrix} y+z & z & y \\ z & z+x & x \\...

The numbers of integral solutions of D = 8, where D = ∣y+zzyzz+xxyxx+y∣\begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix} is-

A

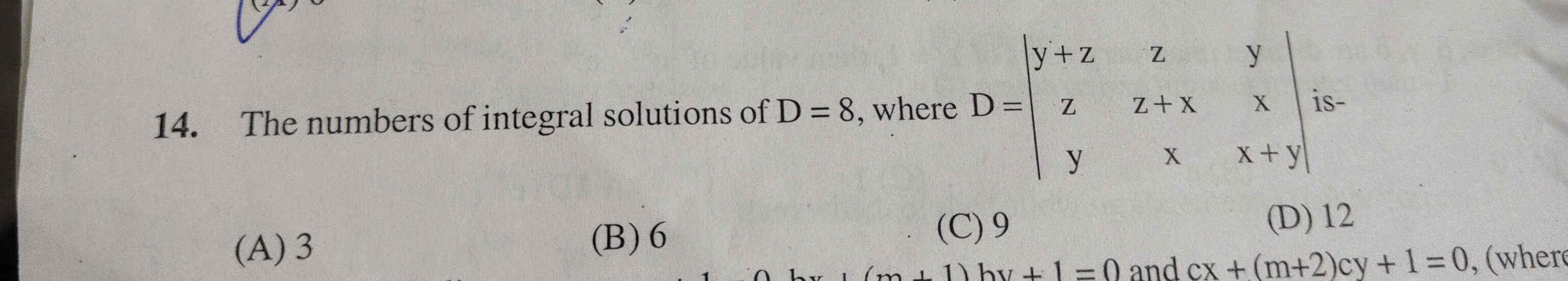
3

B

6

C

9

D

12

Answer

12

Explanation

Solution

The problem asks for the number of integral solutions of D=8D = 8, where DD is a given determinant.

First, let's simplify the determinant DD: D=∣y+zzyzz+xxyxx+y∣D = \begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}

Apply the row operation R1→R1+R2+R3R_1 \rightarrow R_1 + R_2 + R_3: The new first row elements will be: (y+z)+z+y=2y+2z(y+z) + z + y = 2y+2z z+(z+x)+x=2z+2xz + (z+x) + x = 2z+2x y+x+(x+y)=2y+2xy + x + (x+y) = 2y+2x

So, the determinant becomes: D=∣2y+2z2z+2x2y+2xzz+xxyxx+y∣D = \begin{vmatrix} 2y+2z & 2z+2x & 2y+2x \\ z & z+x & x \\ y & x & x+y \end{vmatrix}

Take out the common factor 2 from R1R_1: D=2∣y+zz+xy+xzz+xxyxx+y∣D = 2 \begin{vmatrix} y+z & z+x & y+x \\ z & z+x & x \\ y & x & x+y \end{vmatrix}

Now, apply the row operations R2→R2−R1R_2 \rightarrow R_2 - R_1 and R3→R3−R1R_3 \rightarrow R_3 - R_1: New R2R_2 elements: z−(y+z)=−yz - (y+z) = -y (z+x)−(z+x)=0(z+x) - (z+x) = 0 x−(y+x)=−yx - (y+x) = -y

New R3R_3 elements: y−(y+z)=−zy - (y+z) = -z x−(z+x)=−zx - (z+x) = -z (x+y)−(y+x)=0(x+y) - (y+x) = 0

So, the determinant becomes: D=2∣y+zz+xy+x−y0−y−z−z0∣D = 2 \begin{vmatrix} y+z & z+x & y+x \\ -y & 0 & -y \\ -z & -z & 0 \end{vmatrix}

Now, expand the determinant along R1R_1: D=2[(y+z)∣0−y−z0∣−(z+x)∣−y−y−z0∣+(y+x)∣−y0−z−z∣]D = 2 \left[ (y+z) \begin{vmatrix} 0 & -y \\ -z & 0 \end{vmatrix} - (z+x) \begin{vmatrix} -y & -y \\ -z & 0 \end{vmatrix} + (y+x) \begin{vmatrix} -y & 0 \\ -z & -z \end{vmatrix} \right] D=2[(y+z)(0−yz)−(z+x)(0−yz)+(y+x)(yz−0)]D = 2 \left[ (y+z) (0 - yz) - (z+x) (0 - yz) + (y+x) (yz - 0) \right] D=2[−yz(y+z)+yz(z+x)+yz(y+x)]D = 2 \left[ -yz(y+z) + yz(z+x) + yz(y+x) \right] Take yzyz common from the bracket: D=2yz[−(y+z)+(z+x)+(y+x)]D = 2yz \left[ -(y+z) + (z+x) + (y+x) \right] D=2yz[−y−z+z+x+y+x]D = 2yz \left[ -y-z+z+x+y+x \right] D=2yz[2x]D = 2yz \left[ 2x \right] D=4xyzD = 4xyz

We are given that D=8D = 8. So, 4xyz=84xyz = 8. Dividing by 4, we get xyz=2xyz = 2.

We need to find the number of integral solutions for the equation xyz=2xyz = 2. The integers x,y,zx, y, z can be positive or negative. The product xyz=2xyz = 2 is positive. This means either all three variables are positive, or one is positive and two are negative.

The only set of positive integer magnitudes whose product is 2 is {1,1,2}\{1, 1, 2\}. So, the absolute values (∣x∣,∣y∣,∣z∣)(|x|, |y|, |z|) must be a permutation of (1,1,2)(1, 1, 2).

Let's list the possible ordered triplets (x,y,z)(x, y, z):

Case 1: All three variables are positive. The magnitudes are (1,1,2)(1, 1, 2). The possible permutations are:

  1. (1,1,2)(1, 1, 2)
  2. (1,2,1)(1, 2, 1)
  3. (2,1,1)(2, 1, 1) This gives 3 solutions.

Case 2: One variable is positive, and two variables are negative. The magnitudes are (1,1,2)(1, 1, 2). We need to assign one positive sign and two negative signs.

Subcase 2a: The value with magnitude 2 is positive, and the two values with magnitude 1 are negative. This means the set of values is {2,−1,−1}\{2, -1, -1\}. The possible permutations are:

  1. (2,−1,−1)(2, -1, -1)
  2. (−1,2,−1)(-1, 2, -1)
  3. (−1,−1,2)(-1, -1, 2) This gives 3 solutions.

Subcase 2b: One value with magnitude 1 is positive, and the other value with magnitude 1 and the value with magnitude 2 are negative. This means the set of values is {1,−1,−2}\{1, -1, -2\}. The possible permutations (which are 3!=63! = 6 for distinct numbers) are:

  1. (1,−1,−2)(1, -1, -2)
  2. (1,−2,−1)(1, -2, -1)
  3. (−1,1,−2)(-1, 1, -2)
  4. (−1,−2,1)(-1, -2, 1)
  5. (−2,1,−1)(-2, 1, -1)
  6. (−2,−1,1)(-2, -1, 1) This gives 6 solutions.

Total number of integral solutions = (Solutions from Case 1) + (Solutions from Subcase 2a) + (Solutions from Subcase 2b) Total solutions = 3+3+6=123 + 3 + 6 = 12.