Question
Question: The general solution of the differential equation $\frac{dy}{dx} + x(x+y) = x(x+y)^3 -1$ is:...
The general solution of the differential equation dxdy+x(x+y)=x(x+y)3−1 is:
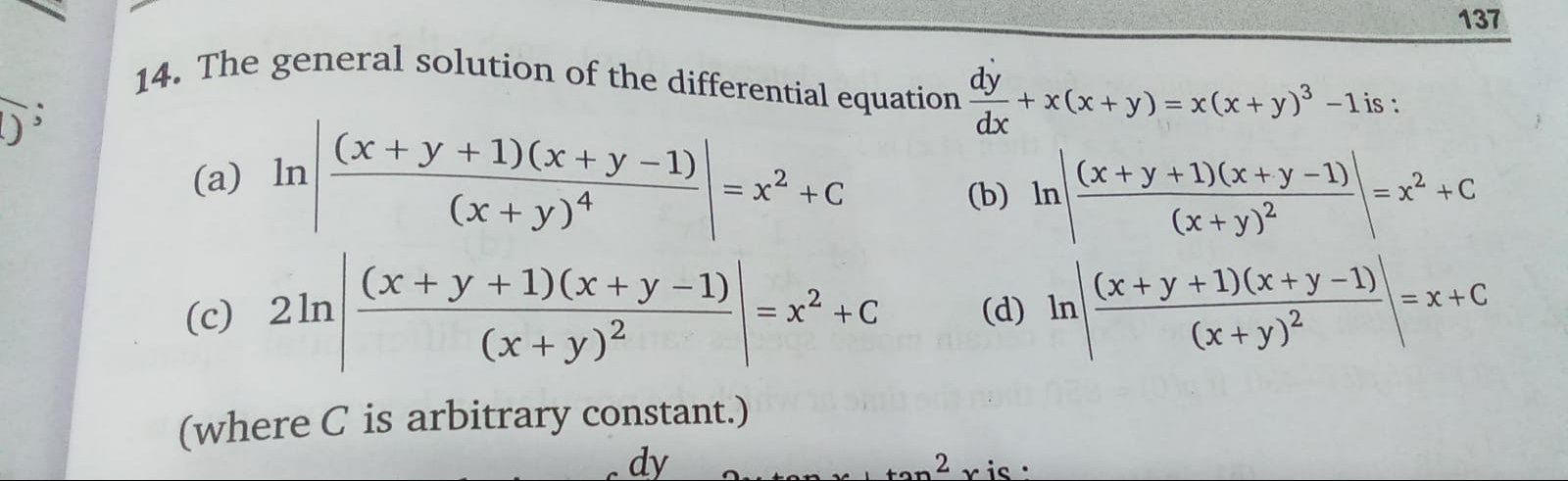
ln(x+y)4(x+y+1)(x+y−1)=x2+C
ln(x+y)2(x+y+1)(x+y−1)=x2+C
2ln(x+y)2(x+y+1)(x+y−1)=x2+C
ln(x+y)2(x+y+1)(x+y−1)=x+C
ln | (x+y+1)(x+y-1) / (x+y)^2 | = x^2 + C
Solution
The given differential equation is: dxdy+x(x+y)=x(x+y)3−1 Rearrange the terms to group the constant with the derivative: dxdy+1+x(x+y)=x(x+y)3 Let v=x+y. Differentiating v with respect to x: dxdv=dxd(x+y)=1+dxdy Substitute v and dxdv into the rearranged differential equation: dxdv+xv=xv3 This is a Bernoulli differential equation of the form dxdv+P(x)v=Q(x)vn, where P(x)=x, Q(x)=x, and n=3.
To solve a Bernoulli equation, divide by vn (in this case, v3): v−3dxdv+xv−2=x Now, let z=v1−n=v1−3=v−2. Differentiate z with respect to x: dxdz=−2v−3dxdv From this, we can express v−3dxdv as −21dxdz. Substitute this into the equation: −21dxdz+xz=x Multiply the entire equation by -2 to convert it into a standard first-order linear differential equation form: dxdz−2xz=−2x This is a linear differential equation of the form dxdz+P′(x)z=Q′(x), where P′(x)=−2x and Q′(x)=−2x.
The integrating factor (I.F.) is given by e∫P′(x)dx: I.F.=e∫−2xdx=e−x2 Multiply the linear differential equation by the integrating factor: e−x2dxdz−2xe−x2z=−2xe−x2 The left side of the equation is the derivative of the product z⋅I.F.: dxd(ze−x2)=−2xe−x2 Now, integrate both sides with respect to x: ∫dxd(ze−x2)dx=∫−2xe−x2dx ze−x2=∫−2xe−x2dx To evaluate the integral on the right side, let u=−x2. Then du=−2xdx. ∫eudu=eu+C1=e−x2+C1 So, the solution in terms of z is: ze−x2=e−x2+C1 Divide by e−x2: z=1+C1ex2 Now, substitute back z=v−2 and v=x+y: (x+y)−2=1+C1ex2 (x+y)21=1+C1ex2 Rearrange the equation to match the options provided: (x+y)21−1=C1ex2 (x+y)21−(x+y)2=C1ex2 Using the difference of squares formula, 1−(x+y)2=(1−(x+y))(1+(x+y)): (x+y)2(1−x−y)(1+x+y)=C1ex2 Take the natural logarithm of both sides. Note that (1−x−y)=−(x+y−1), and since we are taking absolute values, the negative sign outside doesn't affect the result. ln(x+y)2(1−x−y)(1+x+y)=ln∣C1ex2∣ ln(x+y)2(x+y−1)(x+y+1)=ln∣C1∣+ln∣ex2∣ ln(x+y)2(x+y−1)(x+y+1)=x2+C where C=ln∣C1∣ is an arbitrary constant.
Comparing this result with the given options, it matches option (b).
