Solveeit Logo
Login

Question

Question: The following reaction has an equilibrium constant $K_C$ equal to 3.07 x $10^{-4}$ at 24°C. $2NOBr(g...

The following reaction has an equilibrium constant KCK_C equal to 3.07 x 10−410^{-4} at 24°C. 2NOBr(g)⇌2NO(g)+Br2(g)2NOBr(g) \rightleftharpoons 2NO(g) + Br_2(g)

The correct set of concentrations at which the rate of forward reaction is greater than that of backward reaction is

A

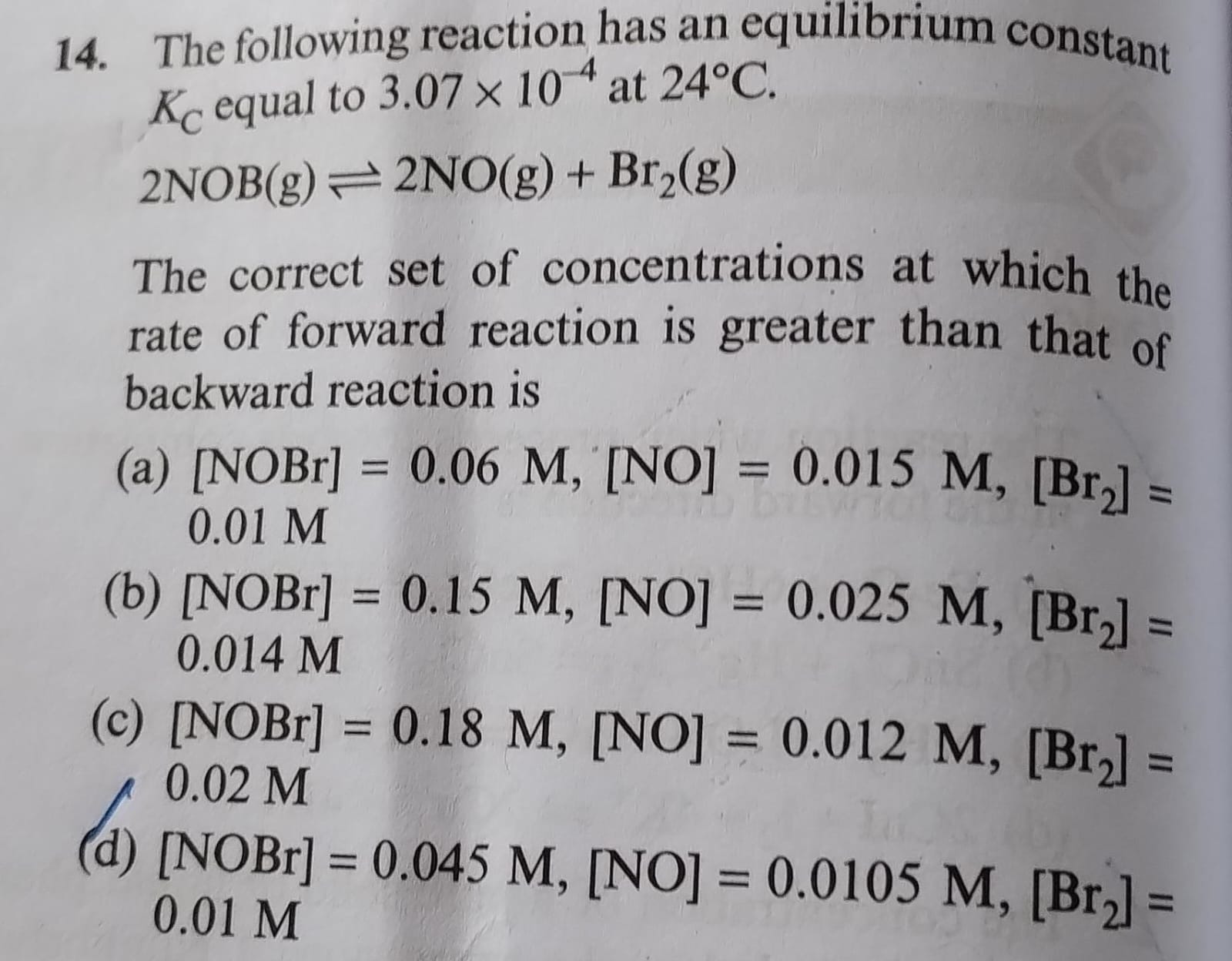
[NOBr] = 0.06 M, [NO] = 0.015 M, [Br2Br_2] = 0.01 M

B

[NOBr] = 0.15 M, [NO] = 0.025 M, [Br2Br_2] = 0.014 M

C

[NOBr] = 0.18 M, [NO] = 0.012 M, [Br2Br_2] = 0.02 M

D

[NOBr] = 0.045 M, [NO] = 0.0105 M, [Br2Br_2] = 0.01 M

Answer

[NOBr] = 0.18 M, [NO] = 0.012 M, [Br2Br_2] = 0.02 M

Explanation

Solution

The rate of the forward reaction is greater than the backward reaction when the reaction quotient (QCQ_C) is less than the equilibrium constant (KCK_C). For the reaction 2NOBr(g)⇌2NO(g)+Br2(g)2NOBr(g) \rightleftharpoons 2NO(g) + Br_2(g), the reaction quotient is QC=[NO]2[Br2][NOBr]2Q_C = \frac{[NO]^2[Br_2]}{[NOBr]^2}. Given KC=3.07×10−4K_C = 3.07 \times 10^{-4}. Calculating QCQ_C for option (c): QC=(0.012)2×0.02(0.18)2=(1.44×10−4)×(2×10−2)3.24×10−2=2.88×10−63.24×10−2≈8.89×10−5Q_C = \frac{(0.012)^2 \times 0.02}{(0.18)^2} = \frac{(1.44 \times 10^{-4}) \times (2 \times 10^{-2})}{3.24 \times 10^{-2}} = \frac{2.88 \times 10^{-6}}{3.24 \times 10^{-2}} \approx 8.89 \times 10^{-5}. Since 8.89×10−5<3.07×10−48.89 \times 10^{-5} < 3.07 \times 10^{-4}, QC<KCQ_C < K_C, indicating the forward reaction rate is greater.