Question

The equation of a progressive wave is, $y=a \sin 2\pi (nt - \frac{x}{5})$. The ratio of maximum particle velocity to wave velocity is

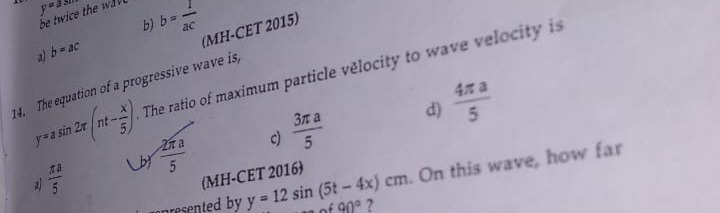
• A. $\frac{\pi a}{5}$
• B. $\frac{2\pi a}{5}$
• C. $\frac{3\pi a}{5}$
• D. $\frac{4\pi a}{5}$

Answer 1

Answer: (B)

$\frac{2\pi a}{5}$

Answer 2

The given wave is

$$y = a \sin\left( 2\pi\left(nt - \frac{x}{5}\right) \right).$$

Step 1: Identify angular frequency and wave number

Rewrite the argument as:

$$2\pi nt - \frac{2\pi}{5}x.$$

Thus,

$$\omega = 2\pi n \quad \text{and} \quad k = \frac{2\pi}{5}.$$

Step 2: Determine wave velocity

The phase (wave) velocity is

$$v = \frac{\omega}{k} = \frac{2\pi n}{2\pi/5} = 5n.$$

Step 3: Find maximum particle velocity

The transverse particle velocity is given by

$$v_y = \frac{\partial y}{\partial t} = a \cdot \cos\left(2\pi\left(nt - \frac{x}{5}\right)\right) \cdot 2\pi n.$$

The maximum value (when $\cos$ term is 1) is:

$$(v_y)_{\text{max}} = 2\pi n a.$$

Step 4: Compute the ratio

$$\frac{(v_y)_{\text{max}}}{v} = \frac{2\pi n a}{5n} = \frac{2\pi a}{5}.$$