Question

The electric field for a electromagnetic wave in free space is $\bar{E}$ = 30 cos (kz - 5 x $10^{8}t$) $\hat{i}$ . The magnitude of wave vector k is (velocity of EM wave in free space = 3 x $10^{8}$ m/s)

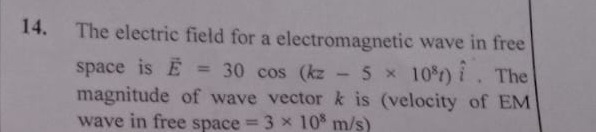
• A. 3/5
• B. 5/3
• C. 3
• D. 5

Answer 1

Answer: (B)

5/3

Answer 2

The electric field of an electromagnetic wave in free space is given by:

$\bar{E} = 30 \cos (kz - 5 \times 10^{8}t) \hat{i}$

Comparing with the general form $\bar{E} = E_0 \cos (kz - \omega t) \hat{i}$, we get $\omega = 5 \times 10^{8}$ rad/s.

The velocity of an electromagnetic wave in free space ($c$) is related to $\omega$ and $k$ by:

$c = \frac{\omega}{k}$

Given $c = 3 \times 10^{8}$ m/s, we can find $k$:

$k = \frac{\omega}{c} = \frac{5 \times 10^{8}}{3 \times 10^{8}} = \frac{5}{3}$ rad/m