Question
Question: The distance between the parallel lines given by $(x+7y)^2+4\sqrt{2}(x+7y)-42=0$...
The distance between the parallel lines given by (x+7y)2+42(x+7y)−42=0
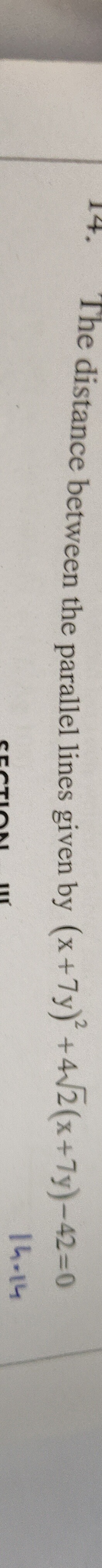
2
Solution
Let Z=x+7y. The given equation becomes a quadratic equation in Z: Z2+42Z−42=0
Solving this quadratic equation for Z using the quadratic formula Z=2a−b±b2−4ac: Z=2(1)−42±(42)2−4(1)(−42) Z=2−42±32+168 Z=2−42±200 Z=2−42±102
This gives two distinct values for Z: Z1=2−42+102=262=32 Z2=2−42−102=2−142=−72
Substituting back Z=x+7y, we obtain the equations of two parallel lines: Line 1: x+7y=32⟹x+7y−32=0 Line 2: x+7y=−72⟹x+7y+72=0
The distance between two parallel lines of the form ax+by+c1=0 and ax+by+c2=0 is given by the formula: d=a2+b2∣c1−c2∣
For our lines, a=1, b=7, c1=−32, and c2=72. d=12+72∣−32−72∣ d=1+49∣−102∣ d=50102 d=52102 d=2
