Solveeit Logo
Login

Question

Question: The distance between parallel lines $\overline{r} = (2i-j+k) + \lambda (2i + j - 2k)$ and $\overline...

The distance between parallel lines r‾=(2i−j+k)+λ(2i+j−2k)\overline{r} = (2i-j+k) + \lambda (2i + j - 2k) and r‾=(i−j+2k)+μ(2i+j−2k)\overline{r} = (i-j+2k) + \mu (2i+j-2k) is

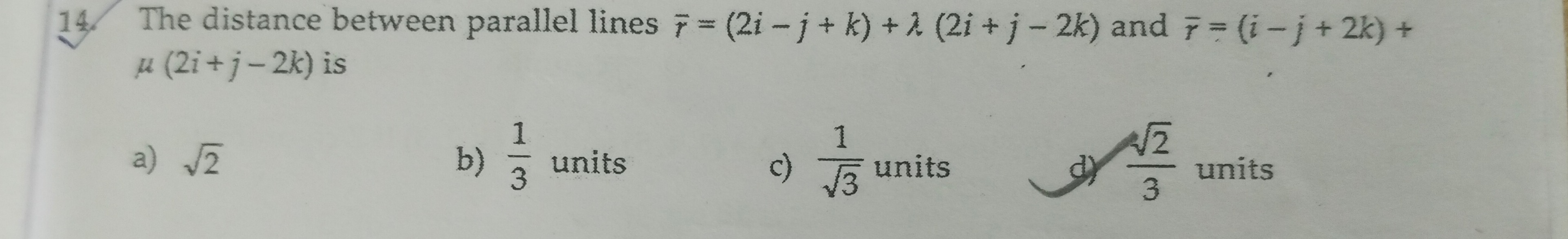
A

2\sqrt{2}

B

13\frac{1}{3} units

C

13\frac{1}{\sqrt{3}} units

D

23\frac{\sqrt{2}}{3} units

Answer

23\frac{\sqrt{2}}{3} units

Explanation

Solution

Solution Explanation:

  1. Write points and direction vector:

    • Line 1: Point A = (2, –1, 1), Direction d = (2, 1, –2)
    • Line 2: Point B = (1, –1, 2), same direction d.

  2. Compute vector AB = B – A = (–1, 0, 1).

  3. Compute cross product:

    AB × d = (–1, 0, 1) × (2, 1, –2) = (0·(–2) – 1·1, 1·2 – (–1)(–2), (–1)·1 – 0·2)

    = (–1, 2–2, –1) = (–1, 0, –1).

  4. Find magnitudes:

    |AB × d| = √(1 + 0 + 1) = √2, |d| = √(4 + 1 + 4) = 3.

  5. Distance = |AB × d| / |d| = (√2)/3.