Question

Locus of all point P(x, y) satisfying x³ + y³ + 3xy = 1 consists of union of

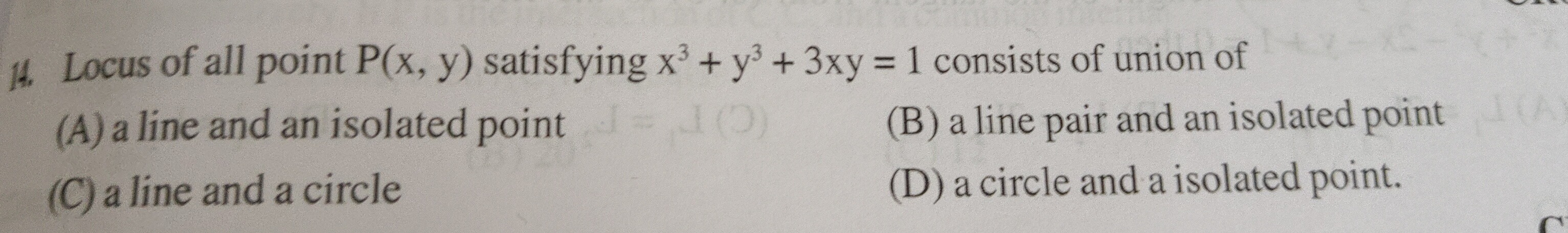
• A. a line and an isolated point
• B. a line pair and an isolated point
• C. a line and a circle
• D. a circle and a isolated point.

Answer 1

Answer: (A)

a line and an isolated point

Answer 2

The given equation is $x^3 + y^3 + 3xy = 1$. We can rewrite this equation as $x^3 + y^3 - 1 + 3xy = 0$.

Using the algebraic identity: $x^3 + y^3 + z^3 - 3xyz = (x+y+z)(x^2+y^2+z^2-xy-yz-zx)$

Let $z = -1$. Substituting this into the identity, we get: $x^3 + y^3 + (-1)^3 - 3xy(-1) = (x+y+(-1))(x^2+y^2+(-1)^2 - xy - y(-1) - (-1)x)$ $x^3 + y^3 - 1 + 3xy = (x+y-1)(x^2+y^2+1 - xy + y + x)$

The given equation $x^3 + y^3 - 1 + 3xy = 0$ is therefore equivalent to: $(x+y-1)(x^2+y^2+1 - xy + y + x) = 0$

This equation is satisfied if either of the factors is zero:

Factor 1: $x+y-1 = 0$ This is the equation of a straight line.

Factor 2: $x^2+y^2+1 - xy + y + x = 0$ To analyze this equation, we can multiply it by 2: $2x^2+2y^2+2 - 2xy + 2y + 2x = 0$ Rearrange the terms to form perfect squares: $(x^2 - 2xy + y^2) + (x^2 + 2x + 1) + (y^2 + 2y + 1) = 0$ This simplifies to: $(x-y)^2 + (x+1)^2 + (y+1)^2 = 0$

For the sum of three squares to be zero, each individual square must be zero:

1. $(x-y)^2 = 0 \implies x-y = 0 \implies x=y$
2. $(x+1)^2 = 0 \implies x+1 = 0 \implies x=-1$
3. $(y+1)^2 = 0 \implies y+1 = 0 \implies y=-1$

The only solution that satisfies all three conditions is $x=-1$ and $y=-1$. Thus, the second equation represents the single isolated point $(-1, -1)$.

The locus of all points P(x, y) satisfying the original equation is the union of the locus of points satisfying the first factor (a line) and the locus of points satisfying the second factor (an isolated point). The point $(-1, -1)$ does not lie on the line $x+y-1=0$, since $-1 + (-1) - 1 = -3 \neq 0$.

Therefore, the locus consists of a line and an isolated point.