Question

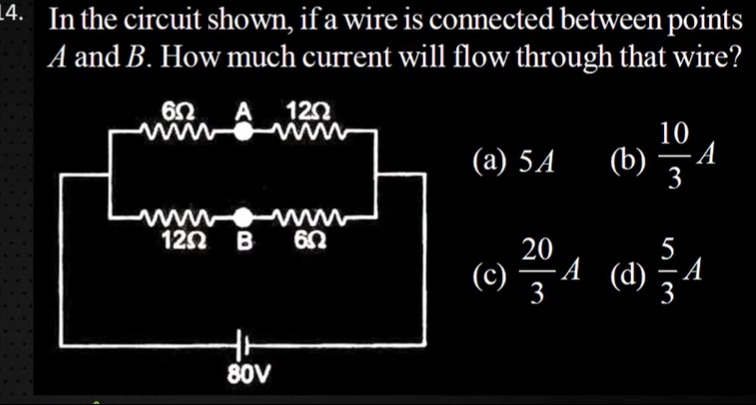
In the circuit shown, if a wire is connected between points $A$ and $B$. How much current will flow through that wire?

• A. 5A
• B. $\frac{10}{3}A$
• C. $\frac{20}{3}A$
• D. $\frac{5}{3}A$

Answer 1

Answer: (B)

$\frac{10}{3}A$

Answer 2

When a wire connects points A and B, their potentials become equal, i.e., $V_A = V_B = V$. Let the left side of the battery be $V_L = 80V$ and the right side be $V_R = 0V$.

Using Kirchhoff's Current Law (KCL) at node A: Current entering A from the left: $I_{LA} = \frac{V_L - V_A}{6\Omega} = \frac{80 - V}{6}$. Current leaving A to the right: $I_{AR} = \frac{V_A - V_R}{12\Omega} = \frac{V}{12}$. Let $I_{AB}$ be the current flowing from A to B. KCL at A: $I_{LA} = I_{AR} + I_{AB} \implies I_{AB} = \frac{80 - V}{6} - \frac{V}{12}$.

Using KCL at node B: Current entering B from the left: $I_{LB} = \frac{V_L - V_B}{12\Omega} = \frac{80 - V}{12}$. Current leaving B to the right: $I_{BR} = \frac{V_B - V_R}{6\Omega} = \frac{V}{6}$. KCL at B: $I_{LB} + I_{AB} = I_{BR}$ (since $I_{AB}$ enters B). $I_{AB} = I_{BR} - I_{LB} = \frac{V}{6} - \frac{80 - V}{12}$.

Equating the two expressions for $I_{AB}$: $\frac{80 - V}{6} - \frac{V}{12} = \frac{V}{6} - \frac{80 - V}{12}$ Multiply by 12: $2(80 - V) - V = 2V - (80 - V)$ $160 - 2V - V = 2V - 80 + V$ $160 - 3V = 3V - 80$ $240 = 6V$ $V = 40V$.

Now, calculate $I_{AB}$: $I_{AB} = \frac{80 - 40}{6} - \frac{40}{12} = \frac{40}{6} - \frac{40}{12} = \frac{20}{3} - \frac{10}{3} = \frac{10}{3}A$.