Question
Question: If $\theta = \frac{\pi}{15}$, then value of $\frac{(\sin 5\theta + \cos 5\theta) + (\sin 7\theta - \...
If θ=15π, then value of (sin8θ+cos8θ)+(sin10θ−cos10θ)(sin5θ+cos5θ)+(sin7θ−cos7θ) is equal to -
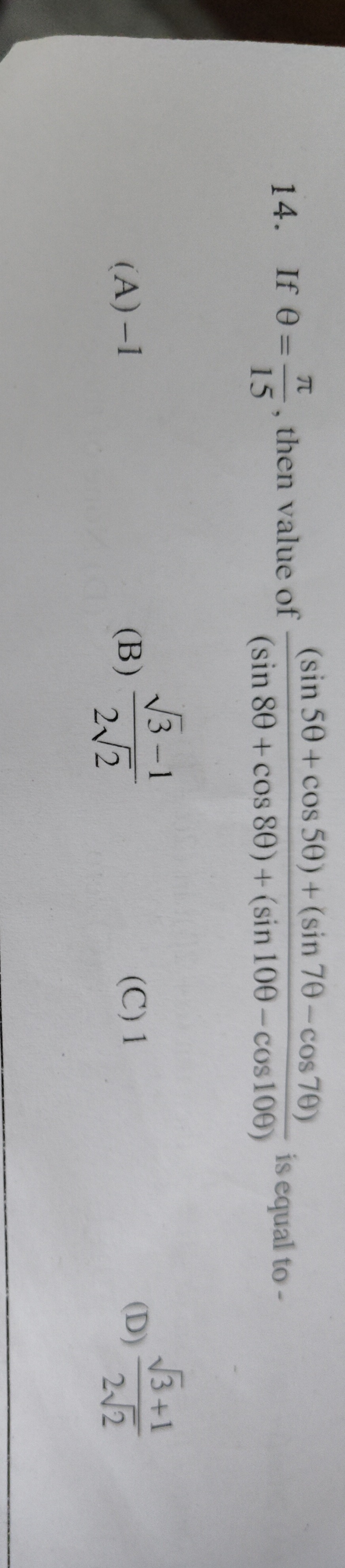
-1
223−1
1
223+1
1
Solution
The problem asks us to find the value of a given trigonometric expression when θ=15π.
Let the given expression be E: E=(sin8θ+cos8θ)+(sin10θ−cos10θ)(sin5θ+cos5θ)+(sin7θ−cos7θ)
First, let's simplify the numerator (N) and the denominator (D) separately.
Step 1: Simplify the Numerator (N) N=(sin5θ+cos5θ)+(sin7θ−cos7θ) Rearrange the terms: N=(sin5θ+sin7θ)+(cos5θ−cos7θ) Apply the sum-to-product formulas: sinA+sinB=2sin(2A+B)cos(2A−B) cosA−cosB=−2sin(2A+B)sin(2A−B)
For the first part (sin5θ+sin7θ): A=5θ,B=7θ 2A+B=25θ+7θ=6θ 2A−B=25θ−7θ=−θ So, sin5θ+sin7θ=2sin(6θ)cos(−θ)=2sin(6θ)cos(θ) (since cos(−x)=cosx)
For the second part (cos5θ−cos7θ): A=5θ,B=7θ 2A+B=6θ 2A−B=−θ So, cos5θ−cos7θ=−2sin(6θ)sin(−θ)=−2sin(6θ)(−sinθ)=2sin(6θ)sin(θ) (since sin(−x)=−sinx)
Substitute these back into N: N=2sin(6θ)cos(θ)+2sin(6θ)sin(θ) Factor out 2sin(6θ): N=2sin(6θ)(cos(θ)+sin(θ))
Step 2: Simplify the Denominator (D) D=(sin8θ+cos8θ)+(sin10θ−cos10θ) Rearrange the terms: D=(sin8θ+sin10θ)+(cos8θ−cos10θ) Apply the sum-to-product formulas:
For the first part (sin8θ+sin10θ): A=8θ,B=10θ 2A+B=28θ+10θ=9θ 2A−B=28θ−10θ=−θ So, sin8θ+sin10θ=2sin(9θ)cos(−θ)=2sin(9θ)cos(θ)
For the second part (cos8θ−cos10θ): A=8θ,B=10θ 2A+B=9θ 2A−B=−θ So, cos8θ−cos10θ=−2sin(9θ)sin(−θ)=−2sin(9θ)(−sinθ)=2sin(9θ)sin(θ)
Substitute these back into D: D=2sin(9θ)cos(θ)+2sin(9θ)sin(θ) Factor out 2sin(9θ): D=2sin(9θ)(cos(θ)+sin(θ))
Step 3: Evaluate the Expression E Now, substitute the simplified N and D back into E: E=2sin(9θ)(cos(θ)+sin(θ))2sin(6θ)(cos(θ)+sin(θ)) Given θ=15π, cos(θ)+sin(θ)=cos(15π)+sin(15π). Since 15π is in the first quadrant, both cos(15π) and sin(15π) are positive, so their sum is not zero. Therefore, we can cancel the common term (cos(θ)+sin(θ)): E=sin(9θ)sin(6θ)
Step 4: Substitute the value of θ Given θ=15π. Calculate 6θ and 9θ: 6θ=6×15π=52π 9θ=9×15π=53π
Substitute these values into E: E=sin(53π)sin(52π) We know that sin(π−x)=sinx. Here, 53π=π−52π. So, sin(53π)=sin(π−52π)=sin(52π).
Substitute this back into the expression for E: E=sin(52π)sin(52π) Since 52π=72∘, sin(52π)=0. Therefore, E=1
The final answer is 1.
Explanation of the solution:
- Simplify Numerator: Group terms (sin5θ+sin7θ) and (cos5θ−cos7θ). Apply sum-to-product formulas sinA+sinB=2sin(2A+B)cos(2A−B) and cosA−cosB=−2sin(2A+B)sin(2A−B). This yields N=2sin(6θ)(cosθ+sinθ).
- Simplify Denominator: Similarly, group terms (sin8θ+sin10θ) and (cos8θ−cos10θ). Apply sum-to-product formulas. This yields D=2sin(9θ)(cosθ+sinθ).
- Simplify Expression: Divide the simplified numerator by the simplified denominator. The common factor 2(cosθ+sinθ) cancels out, leaving E=sin(9θ)sin(6θ).
- Substitute θ: Substitute θ=15π into the simplified expression. This gives 6θ=52π and 9θ=53π. So, E=sin(53π)sin(52π).
- Final Evaluation: Use the identity sin(π−x)=sinx. Since 53π=π−52π, we have sin(53π)=sin(52π). Therefore, E=sin(52π)sin(52π)=1.
