Question
Question: If the roots of the equation $px^2 + qx + r = 0$, where $2p, q, 2r$ are in G.P., are of the form $\a...
If the roots of the equation px2+qx+r=0, where 2p,q,2r are in G.P., are of the form α2,4α−4. Then the value of 2p+4q+7r is:
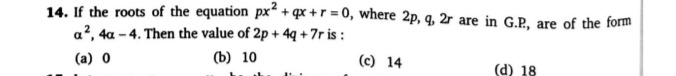
0
10
14
18
The correct answer is not among the given options. The value of the expression is 82p, which is 82 when p=1.
Solution
We start with the quadratic
px2+qx+r=0whose roots are given to be
x1=α2,x2=4α−4.Also, the numbers
2p,q,2rare in a geometric progression (G.P.). (Recall that three numbers a,b,c are in G.P. if and only if b2=ac.)
Step 1. Use Vieta’s formulas.
For the quadratic we have
x1+x2=−pq⟹α2+(4α−4)=−pq,so that
q=−p[α2+4α−4].Also,
x1x2=pr⟹α2(4α−4)=pr,so that
r=pα2(4α−4).Step 2. Use the G.P. condition on 2p,q,2r.
Since these are in G.P.,
q2=(2p)(2r)=4pr.Substitute the expressions for q and r:
[−p(α2+4α−4)]2=4p[pα2(4α−4)].That is,
p2(α2+4α−4)2=4p2α2(4α−4).Since p=0 we cancel p2 to obtain
(α2+4α−4)2=4α2(4α−4).Step 3. Solve for α.
Notice that
4α−4=4(α−1),so the equation becomes
(α2+4α−4)2=16α2(α−1).It is not hard to check that α=2 is a solution. (In fact one may verify that the equation factors as (α−2)4=0 so that α=2 is the unique solution.)
Step 4. Find q and r in terms of p.
Taking α=2 we have
α2+4α−4=4+8−4=8,and4α−4=8−4=4.Thus,
q=−p(8)=−8p,and
r=p(22)(4)=p(4)(4)=16p.Step 5. Compute 2p+4q+7r.
Substitute q=−8p and r=16p:
2p+4q+7r=2p+4(−8p)+7(16p)=2p−32p+112p=(2−32+112)p=82p.Because the quadratic px2+qx+r=0 is determined only up to a nonzero multiplicative constant, one may choose any nonzero value for p. (In other words, the “numerical value” of an expression like 2p+4q+7r — which turns out to be 82p — is only unique if a normalization such as “the quadratic is monic” is imposed; here that would mean taking p=1 so that 2p+4q+7r=82.)
Final remark.
The options given in the problem are
(a) 0 (b) 10 (c) 14 (d) 18.
None of these equals 82. (Also, note that if one simply writes the answer in terms of p, one obtains 82p, which depends on the arbitrary scale factor p.)
Thus, under the usual convention of choosing the quadratic to be monic (i.e. p=1), the value comes out as 82. Since 82 is not one of the options, we conclude that none of the provided options is correct.
