Solveeit Logo
Login

Question

Question: If f(x) = cos⁻¹ x, g(x) = eˣ and h(x) = g(f(x)), then 1 $\frac{h'(x)}{h(x)} =$...

If f(x) = cos⁻¹ x, g(x) = eˣ and h(x) = g(f(x)), then 1

h′(x)h(x)=\frac{h'(x)}{h(x)} =

A

−11−x2\frac{-1}{\sqrt{1-x²}}

B

−(e)(cos−1x)1−x2\frac{-(e)^{(cos^{-1}x)}}{\sqrt{1-x²}}

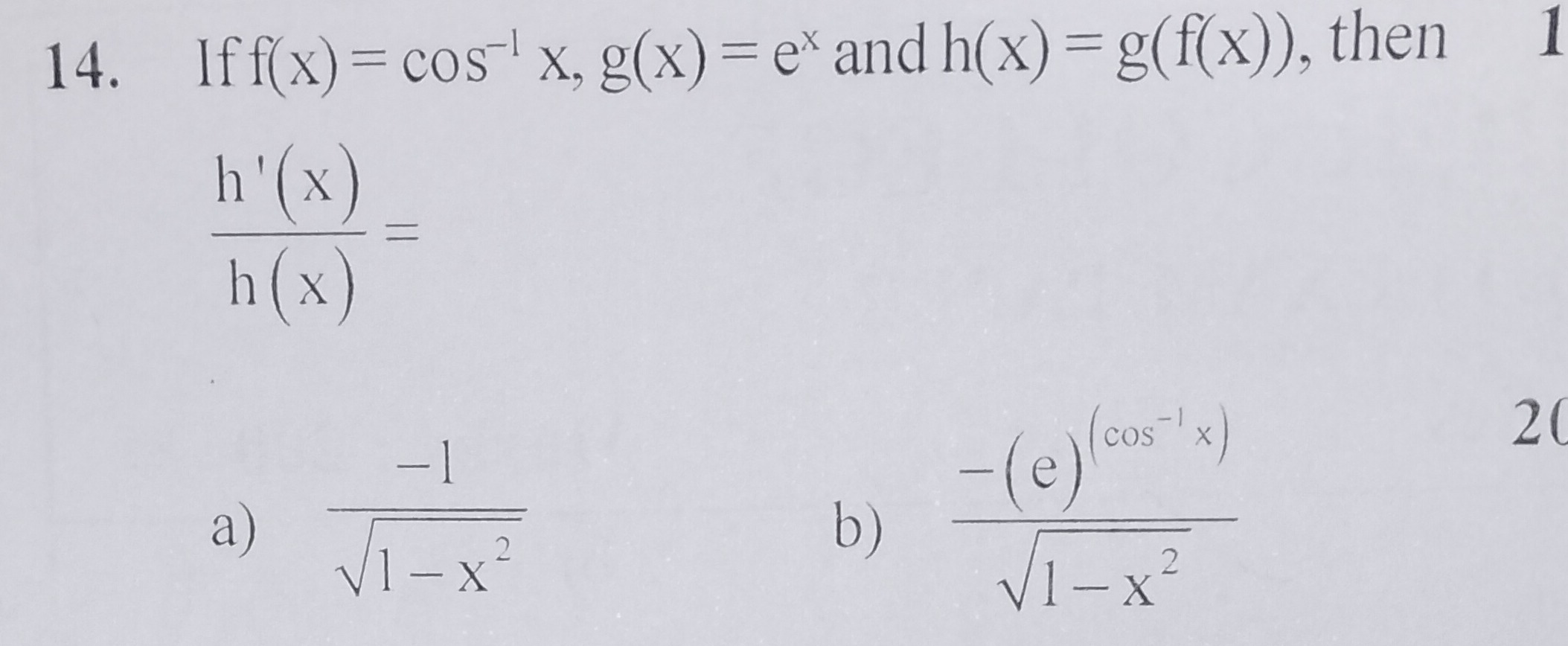
Answer

a) −11−x2\frac{-1}{\sqrt{1-x^2}}

Explanation

Solution

Solution Explanation:

Given:

h(x)=ecos⁡−1(x)h(x) = e^{\cos^{-1}(x)}

Differentiate using the chain rule:

h′(x)=ecos⁡−1(x)⋅ddx(cos⁡−1(x))=ecos⁡−1(x)⋅(−11−x2)h'(x) = e^{\cos^{-1}(x)} \cdot \frac{d}{dx}(\cos^{-1}(x)) = e^{\cos^{-1}(x)} \cdot \left(\frac{-1}{\sqrt{1-x^2}}\right)

Therefore:

h′(x)h(x)=ecos⁡−1(x)⋅(−11−x2)ecos⁡−1(x)=−11−x2\frac{h'(x)}{h(x)} = \frac{e^{\cos^{-1}(x)} \cdot \left(\frac{-1}{\sqrt{1-x^2}}\right)}{e^{\cos^{-1}(x)}} = \frac{-1}{\sqrt{1-x^2}}