Question

Find the largest integral value of 'a' for which every solution of the equation $x([x] - 5) + 2\{x\}+6=0$ satisfies the inequality $(a – 3) x² + 2 (a+3) x-8a ≤ 0$, where

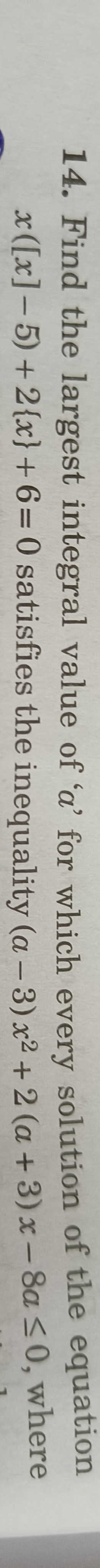
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (A)

1

Answer 2

Let $x = n + \{x\}$, where $n = [x]$ is an integer and $0 \le \{x\} < 1$. The equation is $x([x] - 5) + 2\{x\} + 6 = 0$. Substituting $x = n + \{x\}$: $(n + \{x\})(n - 5) + 2\{x\} + 6 = 0$ $n^2 - 5n + n\{x\} - 5\{x\} + 2\{x\} + 6 = 0$ $n^2 - 5n + 6 + \{x\}(n - 3) = 0$

Case 1: $n - 3 \neq 0$ (i.e., $n \neq 3$) $\{x\}(n - 3) = -(n^2 - 5n + 6) = -(n-2)(n-3)$ Since $n \neq 3$, we can divide by $(n-3)$: $\{x\} = -(n-2) = 2 - n$ We know $0 \le \{x\} < 1$, so $0 \le 2 - n < 1$. Subtracting 2: $-2 \le -n < -1$. Multiplying by -1 and reversing inequalities: $1 < n \le 2$. Since $n$ is an integer, $n=2$. If $n=2$, then $\{x\} = 2 - 2 = 0$. The solution is $x = n + \{x\} = 2 + 0 = 2$.

Case 2: $n - 3 = 0$ (i.e., $n = 3$) The equation becomes $3^2 - 5(3) + 6 + \{x\}(0) = 0$. $9 - 15 + 6 = 0$, which is $0 = 0$. This means for $n=3$, any valid $\{x\}$ works. So, $x = n + \{x\} = 3 + \{x\}$, where $0 \le \{x\} < 1$. This gives the interval $x \in [3, 4)$.

The solutions to the equation are $x=2$ and $x \in [3, 4)$.

Now consider the inequality $(a – 3) x² + 2 (a+3) x-8a ≤ 0$. Let $f(x) = (a – 3) x² + 2 (a+3) x-8a$.

Subcase 2.1: $a - 3 = 0$ (i.e., $a = 3$) The inequality becomes $0x^2 + 2(3+3)x - 8(3) \le 0$, which is $12x - 24 \le 0$, or $x \le 2$. The solutions are $x=2$ and $x \in [3, 4)$. $x=2$ satisfies $x \le 2$. However, for $x \in [3, 4)$, the condition $x \le 2$ is not satisfied. So $a=3$ is not valid.

Subcase 2.2: $a - 3 > 0$ (i.e., $a > 3$) The parabola $f(x)$ opens upwards. For $f(x) \le 0$, $x$ must be between the roots. Let's check if $x=2$ is a root of $f(x)=0$: $f(2) = (a-3)(2^2) + 2(a+3)(2) - 8a = 4(a-3) + 4(a+3) - 8a = 4a - 12 + 4a + 12 - 8a = 0$. So $x=2$ is a root. Let the other root be $r_2$. Sum of roots: $2 + r_2 = -\frac{2(a+3)}{a-3}$. $r_2 = -\frac{2(a+3)}{a-3} - 2 = \frac{-2a-6 - 2(a-3)}{a-3} = \frac{-4a}{a-3}$. For $a > 3$, $a-3 > 0$, so $r_2 = \frac{-4a}{a-3}$ is negative. The roots are $r_2$ (negative) and $2$. $f(x) \le 0$ for $x \in [r_2, 2]$. We need $\{2\} \cup [3, 4) \subseteq [r_2, 2]$. This requires $[3, 4) \subseteq [r_2, 2]$, which is impossible since $3 > 2$. So no solutions for $a > 3$.

Subcase 2.3: $a - 3 < 0$ (i.e., $a < 3$) The parabola $f(x)$ opens downwards. $f(x) \le 0$ for $x$ outside the roots. The roots are $2$ and $r_2 = \frac{-4a}{a-3}$. We need to compare $r_2$ with $2$. $\frac{-4a}{a-3} > 2 \iff \frac{-4a - 2(a-3)}{a-3} > 0 \iff \frac{-6a+6}{a-3} > 0 \iff \frac{6(1-a)}{a-3} > 0$. Since $a < 3$, $a-3 < 0$. For the fraction to be positive, $6(1-a)$ must be negative. $6(1-a) < 0 \implies 1-a < 0 \implies a > 1$. So, if $1 < a < 3$, then $r_2 > 2$. The roots are $2$ and $r_2$. $f(x) \le 0$ for $x \le 2$ or $x \ge r_2$. We need $\{2\} \cup [3, 4) \subseteq (-\infty, 2] \cup [r_2, \infty)$. $x=2$ is covered. For $x \in [3, 4)$, we need $x \le 2$ or $x \ge r_2$. Since $3 > 2$, we must have $x \ge r_2$. This requires $[3, 4) \subseteq [r_2, \infty)$, so $r_2 \le 3$. $\frac{-4a}{a-3} \le 3$. Since $a < 3$, $a-3 < 0$. Multiply by $a-3$ and reverse inequality: $-4a \ge 3(a-3) \implies -4a \ge 3a - 9 \implies 9 \ge 7a \implies a \le \frac{9}{7}$. So, for $1 < a < 3$, we need $a \le \frac{9}{7}$. This gives the range $1 < a \le \frac{9}{7}$.

If $a \le 1$: Then $a < 1$. This implies $1-a > 0$. Since $a < 3$, $a-3 < 0$. $\frac{6(1-a)}{a-3} < 0$, so $r_2 < 2$. The roots are $r_2$ (negative) and $2$. $f(x) \le 0$ for $x \le r_2$ or $x \ge 2$. We need $\{2\} \cup [3, 4) \subseteq (-\infty, r_2] \cup [2, \infty)$. $x=2$ is covered. For $x \in [3, 4)$, we need $x \le r_2$ or $x \ge 2$. Since $3 > 2$, the condition $x \ge 2$ is satisfied. So, all $a \le 1$ are valid.

Combining the valid ranges for $a < 3$: $a \le 1$ and $1 < a \le \frac{9}{7}$. The union is $a \le \frac{9}{7}$. We need the largest integral value of 'a'. Since $\frac{9}{7} \approx 1.28$, the largest integer less than or equal to $\frac{9}{7}$ is $1$.

The largest integral value of 'a' is 1.