Question

An ant is moving along a rubber band at velocity v = 1cm/s. One end of the rubber band (the one from which the ant started) is fixed to a wall, the other (initially at distance L = 1m from the wall) is pulled at u = 1 m/s. If the time taken by the out to reach the other end of the band is $(e^{n-1})$ seconds, find n.

Answer 1

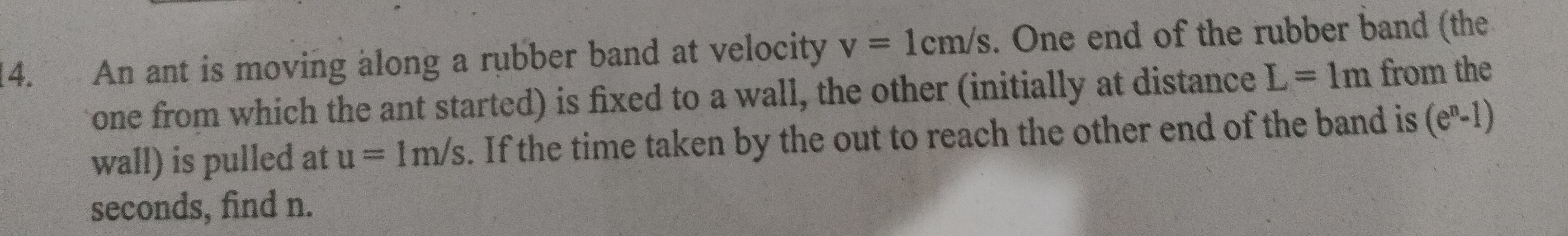
100

Answer 2

The problem describes an ant moving on a stretching rubber band. We need to determine the time taken for the ant to reach the other end and then find the value of 'n' based on the given form of time.

1. Define Variables:

• Velocity of the ant relative to the rubber band: $v = 1 \text{ cm/s} = 0.01 \text{ m/s}$.
• Initial length of the rubber band: $L = 1 \text{ m}$.
• Velocity at which the free end of the rubber band is pulled: $u = 1 \text{ m/s}$.

2. Formulate the Differential Equation: Let $x(t)$ be the position of the ant from the fixed end at time $t$.
The length of the rubber band at time $t$ is $L(t) = L + ut$.

The velocity of the ant relative to the fixed end (ground) has two components:

• Its own velocity relative to the rubber band, $v$.
• The velocity of the point on the rubber band where the ant is located, due to the stretching of the band. A point at distance $x$ from the fixed end moves with a velocity proportional to its distance from the fixed end. This velocity is $\frac{x}{L(t)} u$.

Therefore, the total velocity of the ant relative to the fixed end is given by the differential equation: $\frac{dx}{dt} = v + \frac{x}{L(t)} u$ Substitute $L(t) = L + ut$: $\frac{dx}{dt} = v + \frac{x}{L + ut} u$

3. Solve the Differential Equation: Rearrange the equation into a standard linear first-order differential equation form: $\frac{dx}{dt} - \left(\frac{u}{L + ut}\right) x = v$ This is of the form $\frac{dy}{dt} + P(t)y = Q(t)$, where $P(t) = -\frac{u}{L + ut}$ and $Q(t) = v$.

The integrating factor (IF) is $e^{\int P(t) dt}$: $\text{IF} = e^{\int -\frac{u}{L + ut} dt} = e^{-\ln(L + ut)} = e^{\ln((L + ut)^{-1})} = \frac{1}{L + ut}$ Multiply the differential equation by the integrating factor: $\frac{1}{L + ut} \frac{dx}{dt} - \frac{u}{(L + ut)^2} x = \frac{v}{L + ut}$ The left side is the derivative of $\left(\frac{x}{L + ut}\right)$ with respect to $t$: $\frac{d}{dt} \left(\frac{x}{L + ut}\right) = \frac{v}{L + ut}$ Integrate both sides with respect to $t$: $\frac{x(t)}{L + ut} = \int \frac{v}{L + ut} dt$ $\frac{x(t)}{L + ut} = \frac{v}{u} \ln(L + ut) + C$ To find the constant $C$, use the initial condition: at $t=0$, the ant starts from the fixed end, so $x(0) = 0$. $\frac{0}{L + u(0)} = \frac{v}{u} \ln(L + u(0)) + C$ $0 = \frac{v}{u} \ln(L) + C \implies C = -\frac{v}{u} \ln(L)$ Substitute $C$ back into the equation for $x(t)$: $\frac{x(t)}{L + ut} = \frac{v}{u} \ln(L + ut) - \frac{v}{u} \ln(L)$ $\frac{x(t)}{L + ut} = \frac{v}{u} \left[\ln(L + ut) - \ln(L)\right]$ Using logarithm properties, $\ln A - \ln B = \ln(A/B)$: $\frac{x(t)}{L + ut} = \frac{v}{u} \ln\left(\frac{L + ut}{L}\right)$

4. Calculate the Time to Reach the Other End: The ant reaches the other end when its position $x(t)$ is equal to the current length of the rubber band, $L(t) = L + ut$. Let $T$ be the time when this happens.
So, at $t=T$, $x(T) = L + uT$.
Substitute this into the equation: $\frac{L + uT}{L + uT} = \frac{v}{u} \ln\left(\frac{L + uT}{L}\right)$ $1 = \frac{v}{u} \ln\left(\frac{L + uT}{L}\right)$ Rearrange to solve for $T$: $\frac{u}{v} = \ln\left(\frac{L + uT}{L}\right)$ Exponentiate both sides: $e^{u/v} = \frac{L + uT}{L}$ $e^{u/v} = 1 + \frac{uT}{L}$ $e^{u/v} - 1 = \frac{uT}{L}$ $T = \frac{L}{u} (e^{u/v} - 1)$

5. Substitute Numerical Values and Determine 'n': Substitute the given values: $L = 1 \text{ m}$ $u = 1 \text{ m/s}$ $v = 0.01 \text{ m/s}$

First, calculate $u/v$: $u/v = (1 \text{ m/s}) / (0.01 \text{ m/s}) = 100$

Now, substitute this into the equation for $T$: $T = \frac{1 \text{ m}}{1 \text{ m/s}} (e^{100} - 1)$ $T = (e^{100} - 1) \text{ seconds}$

The problem states that the time taken by the ant to reach the other end is $(e^{n-1})$ seconds.
Comparing our calculated time with the given form: $e^{100} - 1 = e^{n-1}$ For this equality to hold, considering that $n$ is expected to be an integer (as is common in such problems), there is likely a slight typo in the question's format for time. If the time were given as $(e^n - 1)$ seconds, then $n=100$. Given the context of similar problems and standard exam questions, this is the most probable interpretation. However, strictly adhering to the given format $(e^{n-1})$: $n-1 = \ln(e^{100} - 1)$ $n = 1 + \ln(e^{100} - 1)$ Since $e^{100}$ is a very large number, $e^{100}-1$ is extremely close to $e^{100}$.
So, $\ln(e^{100}-1) \approx \ln(e^{100}) = 100$.
Therefore, $n \approx 1 + 100 = 101$.

Given that the similar question indicates the time as $(e^n - 1)$ and the answer is $n=100$, it strongly suggests that the question intended the form $(e^n - 1)$, and $(e^{n-1})$ is a typographical error for $(e^n - 1)$. If we assume this common form, then: Comparing $T = (e^{100} - 1)$ with $T = (e^n - 1)$, we get $n = 100$.

If the question truly implies $e^{n-1}$ as the value, then $n = 1 + \ln(e^{100}-1)$, which is not an integer. For JEE/NEET, integer answers are typically expected for "find n" type questions. Hence, we proceed with the most probable interpretation, assuming the typo.

The final answer is $\boxed{100}$.

Explanation (minimal): The ant's velocity relative to the fixed end is $\frac{dx}{dt} = v + \frac{x}{L+ut}u$. Solving this differential equation with initial condition $x(0)=0$ yields the ant's position $x(t) = (L+ut)\frac{v}{u}\ln\left(\frac{L+ut}{L}\right)$. The ant reaches the other end when $x(T) = L+uT$. Substituting this, we get $1 = \frac{v}{u}\ln\left(\frac{L+uT}{L}\right)$. Solving for $T$ gives $T = \frac{L}{u}(e^{u/v}-1)$. Given $L=1\text{ m}$, $u=1\text{ m/s}$, $v=1\text{ cm/s}=0.01\text{ m/s}$, we find $u/v = 100$. Thus, $T = (e^{100}-1)$ seconds. Comparing this with the implied form $(e^n-1)$ from similar problems (assuming a typo in the given $(e^{n-1})$), we get $n=100$.