Question

A point moves in the xy plane according to the equations $x = a \sin \omega t$ and $y = a \cos \omega t$. The particle has a trajectory

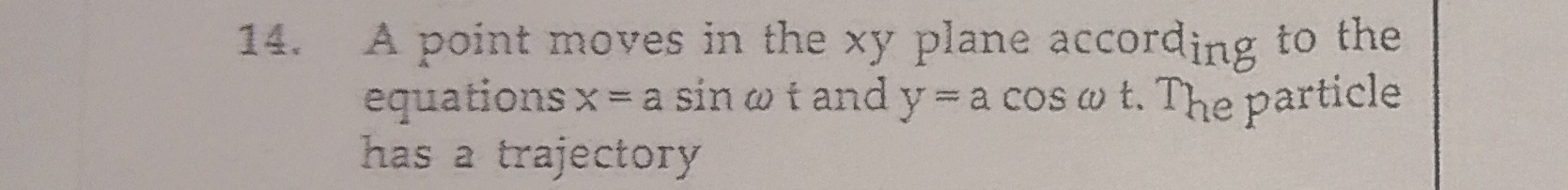
• A. an elliptical path
• B. a circular path
• C. a parabolic path
• D. a straight line path inclined equally to x and y-axes

Answer 1

Answer: (B)

a circular path

Answer 2

Given:

$$x = a\sin\omega t, \quad y = a\cos\omega t$$

Divide both equations by $a$:

$$\frac{x}{a} = \sin\omega t, \quad \frac{y}{a} = \cos\omega t$$

Squaring and adding:

$$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{a}\right)^2 = \sin^2\omega t + \cos^2\omega t = 1$$

Thus,

$$x^2 + y^2 = a^2$$

This is the equation of a circle of radius $a$.