Question

A block of mass m and a pan of equal mass are connected by a string that passes through two ideal pulleys as shown in the figure. Initially when the system is at rest, a putty blob of mass m falls on the pan and sticks to it. If the piece of putty strikes the pan with a speed $v_0$, find the speed with which the block moves just after the collision. Can you apply the principle of conservation of linear momentum knowing that external forces in vertical direction exist? Consider the thread to be perfectly inelastic and almost inextensible.

Answer 1

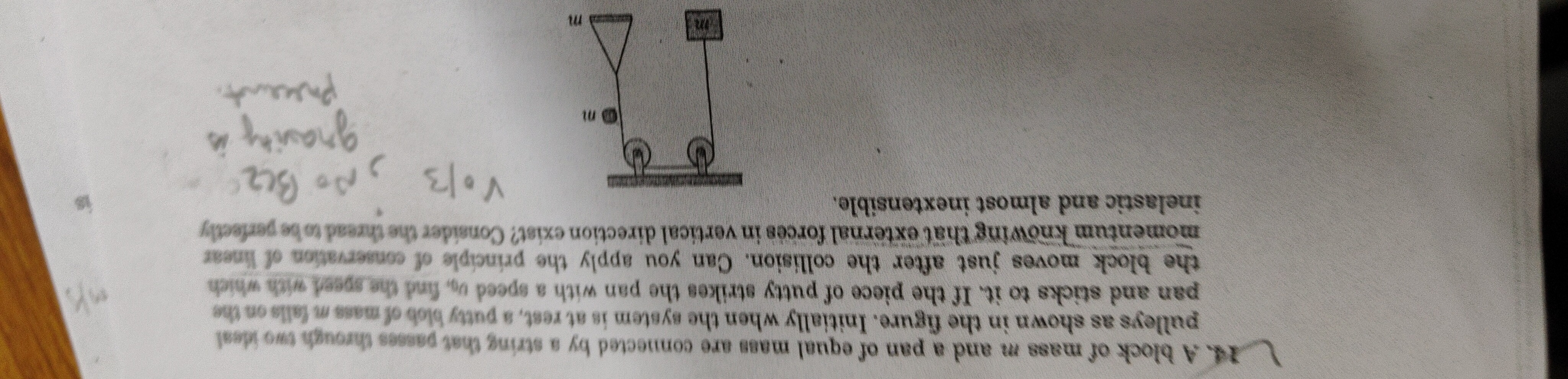
$V_0/3$, No

Answer 2

1. Speed of the block just after the collision:

We use the impulse-momentum theorem for each part of the system. Let v be the common speed of the pan (downwards) and the block (upwards) just after the collision. We consider the collision to be instantaneous, so non-impulsive forces like gravity are neglected during the collision.

• System setup:

  • Mass of block = m
  • Mass of pan = m
  • Mass of putty blob = m
  • Initial speed of putty = v_0 (downwards)
  • Initial speed of pan and block = 0

• Impulse-Momentum for the Putty: Let downwards be the positive direction. Initial momentum of putty: P_i_putty = m * v_0 Final momentum of putty: P_f_putty = m * v The impulse on the putty is due to the normal force N exerted by the pan on the putty (acting upwards). Impulse_putty = P_f_putty - P_i_putty ∫(-N dt) = m * v - m * v_0 (where N is the magnitude of the upward normal force) So, ∫(N dt) = m * v_0 - m * v (This is the magnitude of the upward impulse on the putty, or downward impulse from putty on pan).

• Impulse-Momentum for the Pan: Initial momentum of pan: P_i_pan = 0 Final momentum of pan: P_f_pan = m * v (downwards) Forces on the pan during collision:

  1. Normal force N from putty (downwards).
  2. Tension T from string (upwards). Impulse_pan = P_f_pan - P_i_pan ∫(N dt) - ∫(T dt) = m * v - 0 ∫(N dt) - ∫(T dt) = m * v

• Impulse-Momentum for the Block: Let upwards be the positive direction. Initial momentum of block: P_i_block = 0 Final momentum of block: P_f_block = m * v (upwards) Force on the block during collision: Tension T from string (upwards). Impulse_block = P_f_block - P_i_block ∫(T dt) = m * v - 0 ∫(T dt) = m * v

Now we have a system of equations:

1. ∫(N dt) = m * v_0 - m * v
2. ∫(N dt) - ∫(T dt) = m * v
3. ∫(T dt) = m * v

Substitute equation (3) into equation (2): ∫(N dt) - (m * v) = m * v ∫(N dt) = 2m * v

Now substitute this result into equation (1): 2m * v = m * v_0 - m * v 2m * v + m * v = m * v_0 3m * v = m * v_0 v = \frac{v_0}{3}

2. Applicability of Conservation of Linear Momentum:

The principle of conservation of linear momentum states that the total linear momentum of a system remains constant if the net external force acting on the system is zero, or if the net external impulse during a short time interval (like a collision) is negligible.

Let's consider the system as (putty + pan + block).

• Initial momentum of the system: P_i = m * v_0 (downwards, only putty has initial momentum).
• Final momentum of the system: P_f = (m+m)v (downwards for pan+putty) + mv (upwards for block) P_f = 2mv - mv = mv (downwards).

If linear momentum were conserved, P_i = P_f, which would imply m * v_0 = m * v, leading to v = v_0. However, our calculation shows v = v_0 / 3. This discrepancy indicates that linear momentum for this system is not conserved.

The reason for non-conservation is the presence of significant external impulsive forces. While gravitational forces (3mg on the combined system) are external, their impulse (3mg * dt) over the very short collision time dt is negligible compared to the impulsive forces. The crucial external forces are the reaction forces from the fixed pulley supports. The string exerts a downward force 2T (since there are two segments of string pulling down on the pulleys, each with tension T) on the pulleys. To keep the pulleys fixed, the support exerts an upward reaction force F_support = 2T on the pulleys. This force F_support is external to the system (putty + pan + block). The impulse due to this force is ∫(F_support dt) = ∫(2T dt) = 2 * (mv) = 2mv (upwards). This is a significant external impulse.

Applying the impulse-momentum theorem to the system (putty + pan + block): P_f - P_i = Net External Impulse Let downwards be positive. mv - mv_0 = (Impulse due to gravity) + (Impulse due to pulley support) mv - mv_0 = (negligible) + (-2mv) (since the support impulse 2mv is upwards, it's negative if downwards is positive) mv - mv_0 = -2mv 3mv = mv_0 v = \frac{v_0}{3}

This confirms that the external impulse from the fixed pulley supports prevents the conservation of linear momentum for the system (putty + pan + block).

The answer to the question "Can you apply the principle of conservation of linear momentum knowing that external forces in vertical direction exist?" is No.