Solveeit Logo
Login

Question

Question: 5 \sin^2 x + \sqrt{3} \sin x \cos x + 6 \cos^2 x = 5 if...

5 \sin^2 x + \sqrt{3} \sin x \cos x + 6 \cos^2 x = 5 if

A

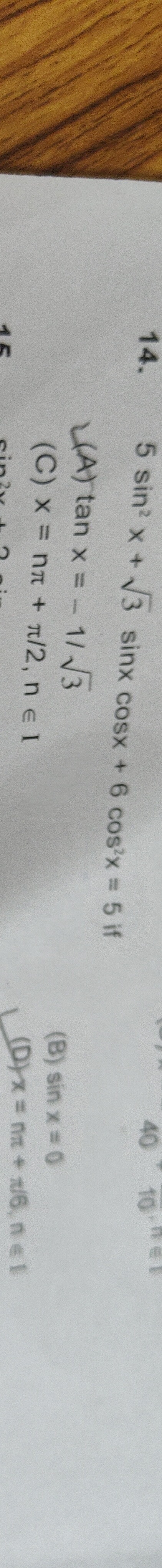
\tan x = -1/\sqrt{3}

B

\sin x = 0

C

x = n\pi + \pi/2, n \in I

D

x = n\pi + \pi/6, n \in I

Answer

A, C

Explanation

Solution

The given trigonometric equation is: 5sin⁡2x+3sin⁡xcos⁡x+6cos⁡2x=55 \sin^2 x + \sqrt{3} \sin x \cos x + 6 \cos^2 x = 5

We know the identity sin⁡2x+cos⁡2x=1\sin^2 x + \cos^2 x = 1. We can rewrite the right side of the equation as 5(sin⁡2x+cos⁡2x)5(\sin^2 x + \cos^2 x). Substituting this into the equation: 5sin⁡2x+3sin⁡xcos⁡x+6cos⁡2x=5(sin⁡2x+cos⁡2x)5 \sin^2 x + \sqrt{3} \sin x \cos x + 6 \cos^2 x = 5(\sin^2 x + \cos^2 x) 5sin⁡2x+3sin⁡xcos⁡x+6cos⁡2x=5sin⁡2x+5cos⁡2x5 \sin^2 x + \sqrt{3} \sin x \cos x + 6 \cos^2 x = 5 \sin^2 x + 5 \cos^2 x

Now, subtract 5sin⁡2x5 \sin^2 x from both sides: 3sin⁡xcos⁡x+6cos⁡2x=5cos⁡2x\sqrt{3} \sin x \cos x + 6 \cos^2 x = 5 \cos^2 x

Subtract 5cos⁡2x5 \cos^2 x from both sides: 3sin⁡xcos⁡x+cos⁡2x=0\sqrt{3} \sin x \cos x + \cos^2 x = 0

Factor out cos⁡x\cos x from the expression: cos⁡x(3sin⁡x+cos⁡x)=0\cos x (\sqrt{3} \sin x + \cos x) = 0

This equation holds true if either of the factors is zero.

Case 1: cos⁡x=0\cos x = 0 The general solution for cos⁡x=0\cos x = 0 is x=nπ+π2x = n\pi + \frac{\pi}{2}, where n∈In \in I (set of integers). This matches option (C). Let's verify this solution with the original equation: If cos⁡x=0\cos x = 0, then sin⁡x=±1\sin x = \pm 1. Substituting into the original equation: 5(±1)2+3(±1)(0)+6(0)2=55(\pm 1)^2 + \sqrt{3}(\pm 1)(0) + 6(0)^2 = 5 5(1)+0+0=55(1) + 0 + 0 = 5 5=55 = 5 This is true, so option (C) is a correct condition.

Case 2: 3sin⁡x+cos⁡x=0\sqrt{3} \sin x + \cos x = 0 To solve this, we can divide by cos⁡x\cos x. We assume cos⁡x≠0\cos x \neq 0 for this step. If cos⁡x=0\cos x = 0, it falls under Case 1. Note that sin⁡x\sin x and cos⁡x\cos x cannot be simultaneously zero. 3sin⁡xcos⁡x+cos⁡xcos⁡x=0\frac{\sqrt{3} \sin x}{\cos x} + \frac{\cos x}{\cos x} = 0 3tan⁡x+1=0\sqrt{3} \tan x + 1 = 0 3tan⁡x=−1\sqrt{3} \tan x = -1 tan⁡x=−13\tan x = -\frac{1}{\sqrt{3}}

This matches option (A). Let's verify this solution with the original equation. If tan⁡x=−1/3\tan x = -1/\sqrt{3}, then x=nπ−π/6x = n\pi - \pi/6. For x=−π/6x = -\pi/6, sin⁡x=−1/2\sin x = -1/2 and cos⁡x=3/2\cos x = \sqrt{3}/2. Substituting into the original equation: 5(−1/2)2+3(−1/2)(3/2)+6(3/2)2=55(-1/2)^2 + \sqrt{3}(-1/2)(\sqrt{3}/2) + 6(\sqrt{3}/2)^2 = 5 5(1/4)+3(−3/4)+6(3/4)=55(1/4) + \sqrt{3}(-3/4) + 6(3/4) = 5 5/4−3/4+18/4=55/4 - 3/4 + 18/4 = 5 (5−3+18)/4=5(5 - 3 + 18)/4 = 5 20/4=520/4 = 5 5=55 = 5 This is true, so option (A) is a correct condition.

Checking other options: (B) sin⁡x=0\sin x = 0: If sin⁡x=0\sin x = 0, then cos⁡x=±1\cos x = \pm 1. Substituting into the original equation: 5(0)2+3(0)(±1)+6(±1)2=55(0)^2 + \sqrt{3}(0)(\pm 1) + 6(\pm 1)^2 = 5 0+0+6(1)=50 + 0 + 6(1) = 5 6=56 = 5, which is false. So (B) is incorrect.

(D) x=nπ+π/6x = n\pi + \pi/6: This implies tan⁡x=tan⁡(π/6)=1/3\tan x = \tan(\pi/6) = 1/\sqrt{3}. This is not equal to −1/3-1/\sqrt{3}, which we found to be a solution. So (D) is incorrect.

Therefore, both options (A) and (C) are correct.