Question

A conducting wire has length 'L₁' and diameter 'd₁'. After stretching the same wire, length becomes 'L₂' and diameter 'd₂'. The ratio of resistances before and after stretching is

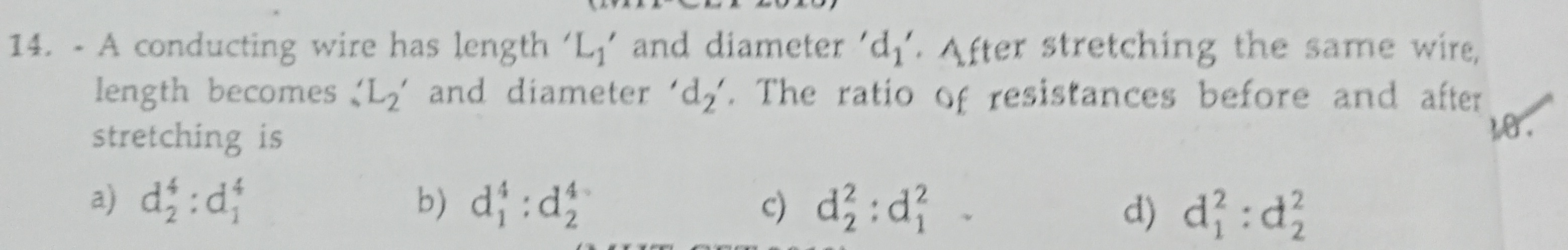
• A. $d_2^4:d_1^4$
• B. $d_1^4:d_2^4$
• C. $d_2^2:d_1^2$
• D. $d_1^2:d_2^2$

Answer 1

Answer: (A)

d_2^4:d_1^4

Answer 2

The resistance of a conducting wire is given by

$$R = \rho \frac{L}{A}$$

where $A$ is the cross-sectional area. Initially,

$$R_1 = \rho \frac{L_1}{A_1}, \quad \text{with } A_1 = \frac{\pi d_1^2}{4}.$$

After stretching,

$$R_2 = \rho \frac{L_2}{A_2}, \quad \text{with } A_2 = \frac{\pi d_2^2}{4}.$$

Since the volume of the wire remains constant,

$$A_1 L_1 = A_2 L_2 \quad \Rightarrow \quad \frac{\pi d_1^2}{4} L_1 = \frac{\pi d_2^2}{4} L_2,$$

which simplifies to

$$d_1^2 L_1 = d_2^2 L_2 \quad \Rightarrow \quad \frac{L_1}{L_2} = \frac{d_2^2}{d_1^2}.$$

Now, expressing $R_1$ and $R_2$:

$$R_1 = \rho \frac{L_1}{\frac{\pi d_1^2}{4}}, \quad R_2 = \rho \frac{L_2}{\frac{\pi d_2^2}{4}}.$$

Taking the ratio,

$$\frac{R_1}{R_2} = \frac{L_1}{L_2} \cdot \frac{d_2^2}{d_1^2}.$$

Substitute $\frac{L_1}{L_2} = \frac{d_2^2}{d_1^2}$:

$$\frac{R_1}{R_2} = \left(\frac{d_2^2}{d_1^2}\right)^2 = \frac{d_2^4}{d_1^4}.$$

Therefore, the ratio of resistances before and after stretching is

$$R_1:R_2 = d_2^4 : d_1^4.$$