Question

A conducting wire has length 'L₁' and diameter 'd₁'. After stretching the same wire, length becomes 'L₂' and diameter 'd₂'. The ratio of resistances before and after stretching is

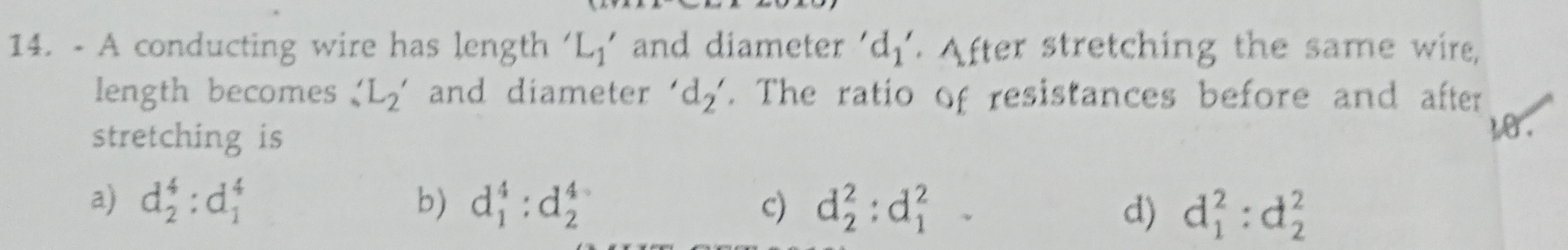
• A. d₂⁴:d₁⁴
• B. d₁⁴:d₂⁴
• C. d₂²:d₁²
• D. d₁²:d₂²

Answer 1

Answer: (A)

d₂⁴:d₁⁴

Answer 2

The ratio of resistances before and after stretching is derived as follows:

1. Initial Resistance: $R_1 = \rho \dfrac{L_1}{A_1}$ $A_1 = \pi \left(\dfrac{d_1}{2}\right)^2 = \dfrac{\pi d_1^2}{4}$ So, $R_1 = \dfrac{4\rho L_1}{\pi d_1^2}$.

2. After Stretching: $R_2 = \dfrac{4\rho L_2}{\pi d_2^2}$.

3. Volume Conservation: Since the volume remains constant: $\dfrac{\pi d_1^2}{4} L_1 = \dfrac{\pi d_2^2}{4} L_2$ $\Rightarrow d_1^2 L_1 = d_2^2 L_2$ $\Rightarrow \dfrac{L_1}{L_2} = \dfrac{d_2^2}{d_1^2}$.

4. Ratio $\dfrac{R_1}{R_2}$:

   $$\dfrac{R_1}{R_2} = \dfrac{ \dfrac{4\rho L_1}{\pi d_1^2}}{\dfrac{4\rho L_2}{\pi d_2^2}} = \dfrac{L_1}{L_2} \cdot \dfrac{d_2^2}{d_1^2} = \left(\dfrac{d_2^2}{d_1^2}\right)^2 = \dfrac{d_2^4}{d_1^4}.$$

Thus, the ratio of resistances before and after stretching is $d_2^4:d_1^4$.