Question
Question: The sum to infinity of the series $\frac{1}{1}+\frac{1}{1+2}+\frac{1}{1+2+3}$ +...... is equal to -...
The sum to infinity of the series 11+1+21+1+2+31 +...... is equal to -
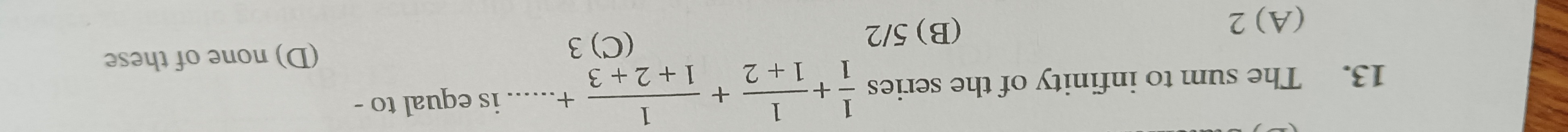
2
5/2
3
none of these
2
Solution
The given series is 11+1+21+1+2+31 +......
First, let's find the general term of the series, Tn. The denominator of the n-th term is the sum of the first n natural numbers, which is given by the formula ∑k=1nk=2n(n+1).
So, the n-th term of the series is: Tn=2n(n+1)1=n(n+1)2
To find the sum to infinity, we need to evaluate S∞=∑n=1∞Tn. We can express Tn using partial fraction decomposition: Tn=n(n+1)2=2(n1−n+11)
Now, let's write out the partial sum SN=∑n=1NTn: SN=∑n=1N2(n1−n+11) SN=2[(11−1+11)+(21−2+11)+(31−3+11)+⋯+(N1−N+11)] SN=2[(1−21)+(21−31)+(31−41)+⋯+(N1−N+11)]
This is a telescoping series, where intermediate terms cancel out. SN=2[1−N+11]
Finally, to find the sum to infinity, we take the limit as N→∞: S∞=limN→∞SN=limN→∞2[1−N+11] As N→∞, N+11 approaches 0. S∞=2[1−0]=2×1=2
The sum to infinity of the series is 2.
