Question

The number of real roots of the equation $(x + 1)(x + 2)(x + 3)(x + 4) + 1 = 0$ is ____.

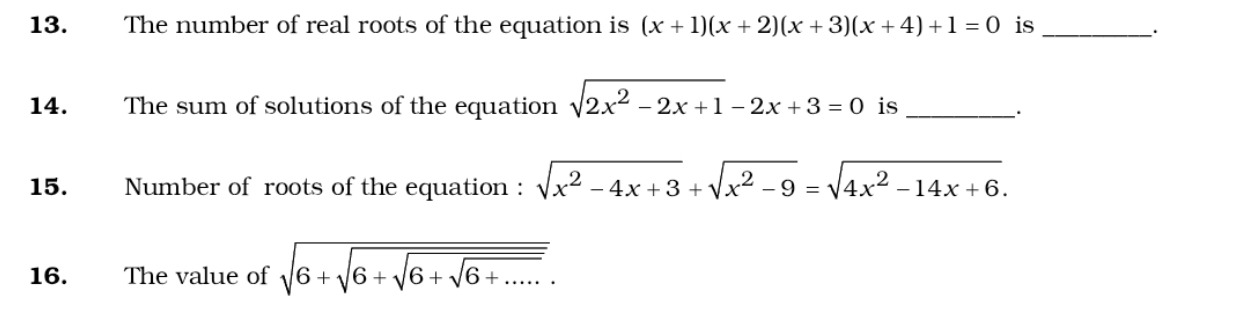
Answer 1

2

Answer 2

We can rearrange the terms to simplify the expression: Group the first and fourth terms, and the second and third terms: $[(x + 1)(x + 4)][(x + 2)(x + 3)] + 1 = 0$ $(x^2 + 5x + 4)(x^2 + 5x + 6) + 1 = 0$

Let $y = x^2 + 5x$. Substituting this into the equation gives: $(y + 4)(y + 6) + 1 = 0$ Expand this equation: $y^2 + 6y + 4y + 24 + 1 = 0$ $y^2 + 10y + 25 = 0$

This is a perfect square trinomial: $(y + 5)^2 = 0$ This implies $y + 5 = 0$, so $y = -5$.

Now substitute back $y = x^2 + 5x$: $x^2 + 5x = -5$ Rearrange into a standard quadratic equation: $x^2 + 5x + 5 = 0$

To find the number of real roots of this quadratic equation, we calculate the discriminant, $\Delta = b^2 - 4ac$. Here, $a=1$, $b=5$, and $c=5$. $\Delta = (5)^2 - 4(1)(5) = 25 - 20 = 5$.

Since $\Delta = 5 > 0$, the quadratic equation has two distinct real roots.