Question

The locus of the foot of the perpendicular from the origin upon chords of the circle x²+y²-2x-4y-4=0, which subtend a right angle at the origin is

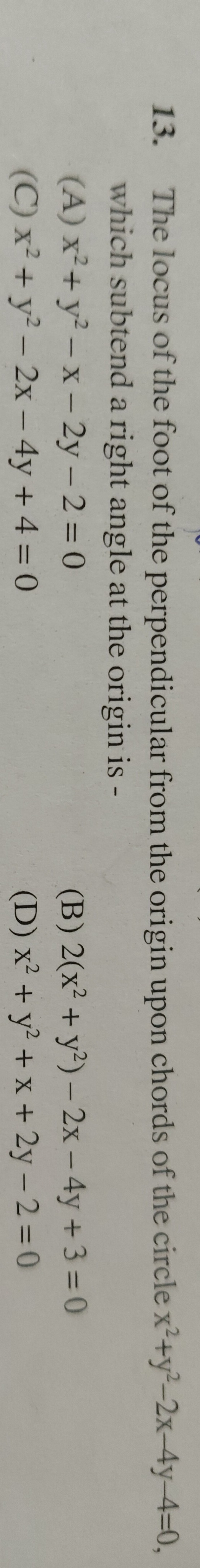
• A. x²+ y² - x - 2y - 2 = 0
• B. 2(x² + y²) - 2x - 4y + 3 = 0
• C. x² + y² - 2x – 4y + 4 = 0
• D. x2 + y² + x + 2y - 2 = 0

Answer 1

Answer: (A)

x²+ y² - x - 2y - 2 = 0

Answer 2

Let the given circle be $C_1: x^2+y^2-2x-4y-4=0$. The general form of a circle is $x^2+y^2+2gx+2fy+c=0$. Comparing the given equation with the general form, we have $g=-1$, $f=-2$, and $c=-4$.

A standard result states that the locus of the foot of the perpendicular from the origin to chords of the circle $x^2+y^2+2gx+2fy+c=0$ which subtend an angle $2\alpha$ at the origin is given by the equation: $x^2+y^2+2gx+2fy+c \cos^2 \alpha = 0$.

In this problem, the angle subtended by the chords at the origin is $90^\circ$. So, $2\alpha = 90^\circ$, which implies $\alpha = 45^\circ$. Therefore, $\cos^2 \alpha = \cos^2 45^\circ = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}$.

Substituting the values of $g$, $f$, $c$, and $\cos^2 \alpha$ into the locus formula: $x^2+y^2+2(-1)x+2(-2)y+(-4)\left(\frac{1}{2}\right) = 0$ $x^2+y^2-2x-4y-2 = 0$.

This equation represents the locus of the foot of the perpendicular from the origin.