Question
Question: 13. The general solution of the equation $\sin 2\theta = \frac{\sqrt{5}-1}{4}$ is...
- The general solution of the equation sin2θ=45−1 is
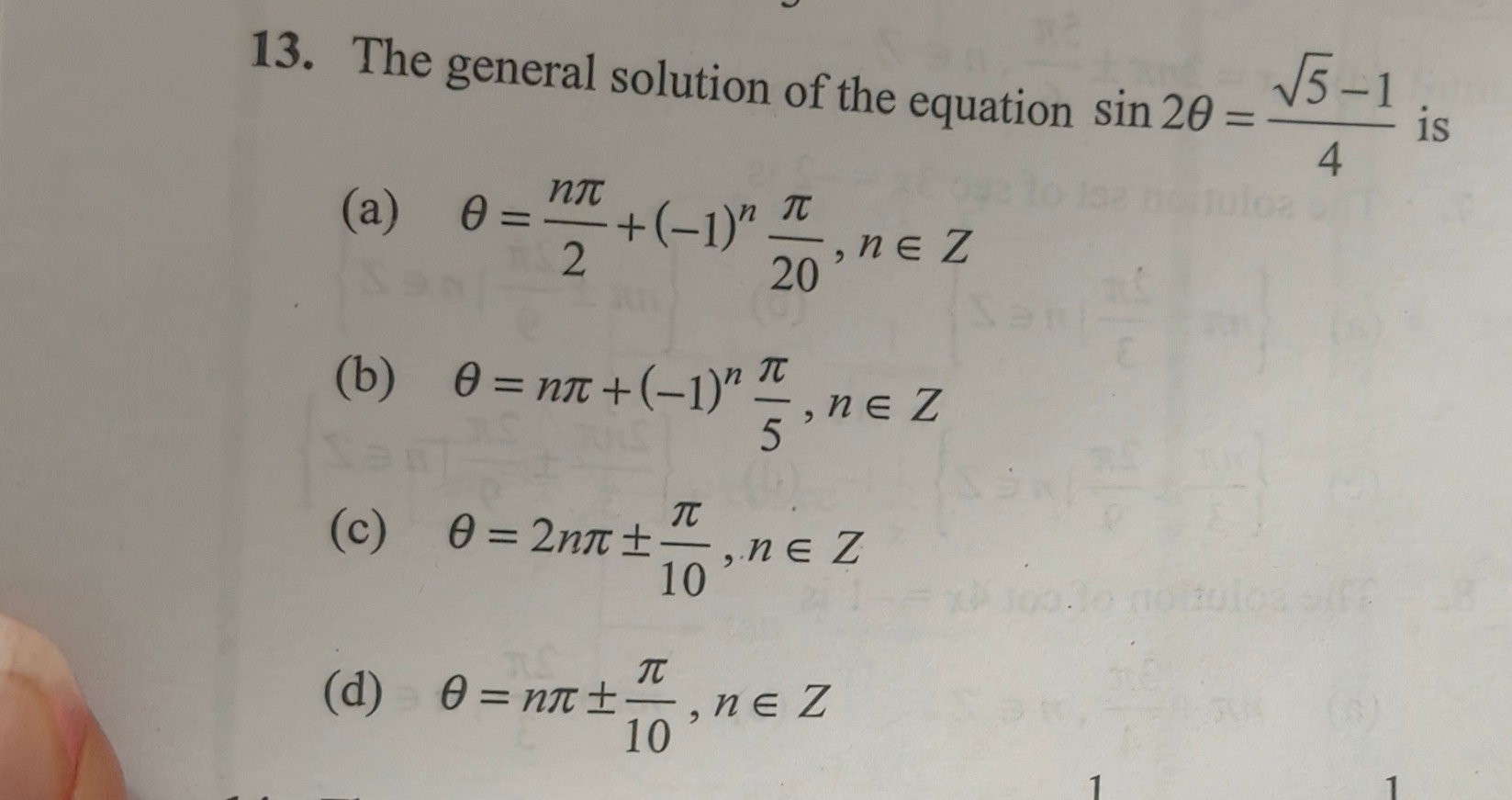
A
θ=2nπ+(−1)n20π,n∈Z
B
θ=nπ+(−1)n5π,n∈Z
C
θ=2nπ±10π,n∈Z
D
θ=nπ±10π,n∈Z
Answer
(a) θ=2nπ+(−1)n20π,n∈Z
Explanation
Solution
Given:
sin2θ=45−1Recognize that
45−1=sin18∘=sin(10π)So,
sin2θ=sin(10π)This gives the solutions for 2θ:
2θ=10π+2πkor2θ=π−10π+2πk,k∈ZThat is,
2θ=10π+2πkor2θ=109π+2πkDividing by 2:
θ=20π+πkorθ=209π+πk,k∈ZThese can be combined into the compact form:
θ=2nπ+(−1)n20π,n∈Zwhich is equivalent to option (a).
