Question
Question: The coefficient of $x^{\frac{n^2+n-14}{2}}$ in $(x-1)(x^2-2)(x^3-3)(x^4-4)...(x^n-n)$, $n \geq 30$ i...
The coefficient of x2n2+n−14 in (x−1)(x2−2)(x3−3)(x4−4)...(xn−n), n≥30 is equal to
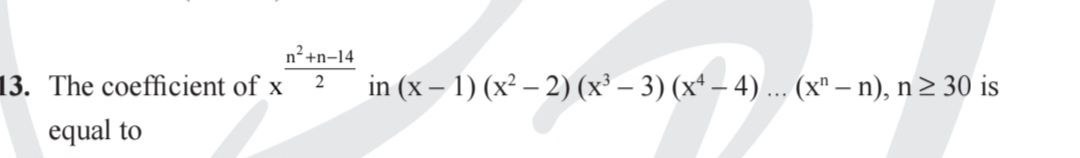
13
Solution
The given expression is P(x)=(x−1)(x2−2)(x3−3)(x4−4)...(xn−n). We need to find the coefficient of x2n2+n−14.
Let's consider a general term in the expansion of P(x). Each term is formed by picking either xk or −k from each factor (xk−k). Let S be the set of indices k for which we choose xk. Let S′ be the set of indices k for which we choose −k. Then S∪S′={1,2,...,n} and S∩S′=∅.
The power of x in such a term will be ∑k∈Sk. The coefficient of this term will be ∏k∈S′(−k).
The maximum possible power of x in the product is when we pick xk from every factor, which is ∑k=1nk=2n(n+1).
The given power of x is 2n2+n−14. We can write this as 2n(n+1)−7.
The power of x in a general term is ∑k∈Sk. Also, ∑k∈Sk=(∑k=1nk)−(∑k∈S′k). Comparing this with the given power: 2n(n+1)−∑k∈S′k=2n(n+1)−7. This implies that ∑k∈S′k=7.
We need to find all possible sets S′ of distinct positive integers whose sum is 7. Since n≥30, all integers from 1 to 7 are available as indices.
Let's list the possible sets S′ and the corresponding coefficients:
-
S′ contains one element: The only possibility is S′={7}. The coefficient is (−1)1⋅7=−7.
-
S′ contains two distinct elements: Let the elements be k1,k2 such that k1+k2=7 and k1=k2. Possible sets:
- S′={1,6}. The coefficient is (−1)2⋅(1⋅6)=6.
- S′={2,5}. The coefficient is (−1)2⋅(2⋅5)=10.
- S′={3,4}. The coefficient is (−1)2⋅(3⋅4)=12.
-
S′ contains three distinct elements: Let the elements be k1,k2,k3 such that k1+k2+k3=7 and k1,k2,k3 are distinct. The only possibility is S′={1,2,4} (since 1+2+3=6, the next smallest is 1+2+4=7). The coefficient is (−1)3⋅(1⋅2⋅4)=−8.
-
S′ contains four or more distinct elements: The smallest sum of four distinct positive integers is 1+2+3+4=10, which is greater than 7. Therefore, no sets with four or more elements are possible.
To find the total coefficient of x2n2+n−14, we sum the coefficients from all valid cases: Total coefficient = (−7)+6+10+12+(−8) Total coefficient = −7+6+10+12−8 Total coefficient = −1+10+12−8 Total coefficient = 9+12−8 Total coefficient = 21−8 Total coefficient = 13.
The final answer is 13.
Explanation of the solution:
The problem asks for the coefficient of a specific power of x in the expansion of a product of terms (xk−k). Each term in the expanded polynomial is formed by choosing either xk or −k from each factor (xk−k). The maximum possible power of x is ∑k=1nk=2n(n+1). The target power of x is 2n(n+1)−7. This means that from the factors (xk−k), we must have chosen −k for a set of indices S′ such that their sum ∑k∈S′k=7. The coefficient for such a term is ∏k∈S′(−k). We enumerate all distinct sets S′ of positive integers that sum to 7:
- {7}: Coefficient =(−7)
- {1,6}: Coefficient =(−1)(−6)=6
- {2,5}: Coefficient =(−2)(−5)=10
- {3,4}: Coefficient =(−3)(−4)=12
- {1,2,4}: Coefficient =(−1)(−2)(−4)=−8 The sum of these coefficients is −7+6+10+12−8=13.
Answer:
The coefficient of x2n2+n−14 is 13. The option is not given, but the calculated value is 13.
